Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T04:53:43.314Z Has data issue: false hasContentIssue false
  • English
  • Français

Conflict-Free Colourings of Uniform Hypergraphs With Few Edges

Published online by Cambridge University Press:  20 April 2012

A. KOSTOCHKA ,
M. KUMBHAT  and
T. ŁUCZAK
A. KOSTOCHKA
Affiliation:
University of Illinois, Urbana, IL 61801, USA and Sobolev Institute of Mathematics, Novosibirsk, 630090, Russia (e-mail: [email protected])
M. KUMBHAT
Affiliation:
Department of Mathematics, University of Illinois, Urbana, IL 61801, USA. (e-mail: [email protected])
T. ŁUCZAK
Affiliation:
Faculty of Mathematics and Computer Science, Adam Mickiewicz University, ul. Umultowska 87, 61-614 Poznań, Poland (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

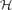A colouring of the vertices of a hypergraph is called conflict-free if each edge e of 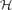contains a vertex whose colour does not repeat in e. The smallest number of colours required for such a colouring is called the conflict-free chromatic number of 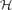, and is denoted by χCF(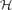). Pach and Tardos proved that for an (2r − 1)-uniform hypergraph 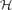with m edges, χCF(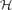) is at most of the order of rm1/r log m, for fixed r and large m. They also raised the question whether a similar upper bound holds for r-uniform hypergraphs. In this paper we show that this is not necessarily the case. Furthermore, we provide lower and upper bounds on the minimum number of edges of an r-uniform simple hypergraph that is not conflict-free k-colourable.

Keywords

Primary 05C1505C35
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 21 , Issue 4 , July 2012 , pp. 611 - 622
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N. (1985) Hypergraphs with high chromatic number, Graphs Combin. 1 387–389.CrossRefGoogle Scholar
[2]Alon, N. and Smorodinsky, S. (2006) Conflict-free colorings of shallow discs. In 22nd Annual ACM Symposium on Computational Geometry, pp. 41–43.CrossRefGoogle Scholar
[3]Bar-Noy, A., Cheilaris, P., Olonetsky, S. and Smorodinsky, S. (2007) Online conflict-free colorings for hypergraphs. In Automata, Languages and Programming, Vol. 4596 of Lecture Notes in Computer Science, Springer, pp. 219–230,CrossRefGoogle Scholar
[4]Bar-Noy, A., Cheilaris, P. and Smorodinsky, S. (2008) Deterministic conflict-free coloring for intervals: From offline to online. ACM Trans. Algorithms 4 #44.CrossRefGoogle Scholar
[5]Beck, J. (1978) On 3-chromatic hypergraphs. Discrete Math. 24 127–137.CrossRefGoogle Scholar
[6]Chen, K., Fiat, A., Kaplan, H., Levy, M., Matoušek, J., Mossel, E., Pach, J.Sharir, M., Smorodinsky, S.Wagner, U. and Welzl, E. (2006/07) Online conflict-free coloring for intervals. SIAM J. Comput. 36 1342–1359.CrossRefGoogle Scholar
[7]Erdős, P. and Lovász, L. (1975) Problems and results on 3-chromatic hypergraphs and some related questions. In Infinite and Finite Sets (Hajnal, A., Rado, R. and Sós, V. T., eds), Vol. 11 of Colloq. Math. Soc. J. Bolyai, North-Holland, pp. 609–627.Google Scholar
[8]Even, G., Lotker, Z., Ron, D. and Smorodinsky, S. (2003) Conflict-free colorings of simple geometric regions with applications to frequency assignment in cellular networks. SIAM J. Comput. 33 94–136.CrossRefGoogle Scholar
[9]Har-Peled, S. and Smorodinsky, S. (2005) Conflict-free coloring of points and simple regions in the plane. Discrete Comput. Geom. 34 47–70.CrossRefGoogle Scholar
[10]Huxley, M. N. and Iwaniec, H. (1975) Bombieri's theorem in short intervals. Mathematika 22 188–194.CrossRefGoogle Scholar
[11]Kostochka, A. V., Kumbhat, M. and Rödl, V. (2010) Coloring uniform hypergraphs with small edge degrees. In Fete of Combinatorics and Computer Science, Vol. 20, Bolyai Society Mathematical Studies, pp. 213–238.CrossRefGoogle Scholar
[12]Pach, J. and Tardos, G. (2009) Conflict-free colorings of graphs and hypergraphs. Combin. Probab. Comput. 18 819–834.CrossRefGoogle Scholar
[13]Pach, J. and Tóth, G. (2003) Conflict-free colorings. In Discrete and Computational Geometry, Springer, Algorithms Combin. 25665–671.CrossRefGoogle Scholar
[14]Radhakrishnan, J. and Srinivasan, A. (2000) Improved bounds and algorithms for hypergraph two-coloring. Random Struct. Alg. 16 4–32.3.0.CO;2-2>CrossRefGoogle Scholar
[15]Spencer, J. (1981) Coloring n-sets red and blue. J. Combin. Theory Ser. A 30 112–113.CrossRefGoogle Scholar