Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T18:06:30.773Z Has data issue: false hasContentIssue false
  • English
  • Français

Combinatorial Structures on van der Waerden sets

Part of: Extremal combinatorics

Published online by Cambridge University Press:  09 January 2015

KONSTANTINOS TYROS
KONSTANTINOS TYROS*
Affiliation:
Mathematics Institute, University of Warwick, Coventry, CV4 7AL, UK (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we provide two results. The first one consists of an infinitary version of the Furstenberg–Weiss theorem. More precisely we show that every subset A of a homogeneous tree T such that

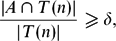$\frac{|A\cap T(n)|}{|T(n)|}\geqslant\delta,$
where T(n) denotes the nth level of T, for all n in a van der Waerden set, for some positive real δ, contains a strong subtree having a level set which forms a van der Waerden set.

The second result is the following. For every sequence (mq)q∈ℕ of positive integers and for every real 0 < δ ⩽ 1, there exists a sequence (nq)q∈ℕ of positive integers such that for every D ⊆ ∪k ∏q=0k-1[nq] satisfying

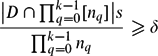$\frac{\big|D\cap \prod_{q=0}^{k-1} [n_q]\big|s}{\prod_{q=0}^{k-1}n_q}\geqslant\delta$
for every k in a van der Waerden set, there is a sequence (Jq)q∈ℕ, where Jq is an arithmetic progression of length mq contained in [nq] for all q, such that ∏q=0k-1Jq ⊆ D for every k in a van der Waerden set. Moreover, working in an abstract setting, we may require Jq to be any configuration of natural numbers that can be found in an arbitrary set of positive density.

MSC classification

Primary: 05D10: Ramsey theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 24 , Issue 6 , November 2015 , pp. 929 - 953
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bergelson, V. and Leibman, A. (1996) Polynomial extensions of van der Waerden's and Szemerédi's theorems. J. Amer. Math. Soc. 9 725–753.Google Scholar
[2] Bergelson, V. and McCutcheon, R. (2000) An Ergodic IP Polynomial Szemerédi Theorem, Vol. 146 of Memoirs of the American Mathematical Society, AMS.Google Scholar
[3] Di Prisco, C. A., Llopis, J. and Todorcevic, S. (2004) Parametrized partitions of products of finite sets. Combinatorica 24 209–232.CrossRefGoogle Scholar
[4] Dodos, P., Kanellopoulos, V. and Tyros, K. A. (2014) Density version of the Carlson–Simpson theorem. J. Eur. Math. Soc. (JEMS) 16 (10) 2097–2164.CrossRefGoogle Scholar
[5] Erdős, P. (1964) On extremal problems of graphs and generalized graphs. Israel J. Math. 2 183–190.Google Scholar
[6] Erdős, P. and Spencer, J. (1974) Probabilistic Methods in Combinatorics, Academic Press.Google Scholar
[7] Frantzikinakis, N. and Wierdl, M. (2009) A Hardy field extension of Szemerédi's theorem. Adv. Math. 222 1–43.Google Scholar
[8] Furstenberg, H. and Weiss, B. (2003) Markov processes and Ramsey theory for trees. Combin. Probab. Comput. 12 547–563.CrossRefGoogle Scholar
[9] Gowers, W. T. (2001) A new proof of Szemerédi's theorem. Geom. Funct. Anal. 11 465–588.Google Scholar
[10] Graham, R. L., Rothschild, B. L. and Spencer, J. H. (1990) Ramsey Theory, second edition, Wiley.Google Scholar
[11] McCutcheon, R. (2010) A variant of the density Hales–Jewett theorem. Bull. Lond. Math. Soc. 42 974–980.Google Scholar
[12] McCutcheon, R. (1999) Elemental methods in ergodic Ramsey theory. Vol. 1722 of Lecture Notes in Mathematics, Springer.Google Scholar
[13] Milliken, K. (1979) A Ramsey theorem for trees. J. Combin. Theory Ser. A 26 215–237.CrossRefGoogle Scholar
[14] Milliken, K. (1981) A partition theorem for the infinite subtrees of a tree. Trans. Amer. Math. Soc. 263 137–148.Google Scholar
[15] Pach, J., Solymosi, J. and Tardos, G. (2012) Remarks on a Ramsey theory for trees. Combinatorica 32 473–482.Google Scholar
[16] Szemerédi, E. (1975) On sets of integers containing no k elements in arithmetic progression. Acta Arithmetica 27 199–245.Google Scholar
[17] Todorcevic, S. (2010) Introduction to Ramsey Spaces, Vol. 174 of Annals of Mathematics Studies, Princeton University Press.CrossRefGoogle Scholar
[18] Todorcevic, S. and Tyros, K. (2013) Subsets of products of finite sets of positive upper density. J. Combin. Theory Ser. A 120 183–193.Google Scholar
[19] van der Waerden, B. L. (1927) Beweis einer Baudetscen Vermuting. Nieuw Arch. Wisk. 15 212–216.Google Scholar