Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T19:10:33.001Z Has data issue: false hasContentIssue false
  • English
  • Français

Balls-in-Bins Processes with Feedback and Brownian Motion

Published online by Cambridge University Press:  01 January 2008

ROBERTO OLIVEIRA
ROBERTO OLIVEIRA*
Affiliation:
IBM T.J. Watson Research Center, Yorktown Heights, NY 10598, USA (e-mail: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In a balls-in-bins process with feedback, balls are sequentially thrown into bins so that the probability that a bin with n balls obtains the next ball is proportional to f(n) for some function f. A commonly studied case where there are two bins and f(n) = np for p > 0, and our goal is to study the fine behaviour of this process with two bins and a large initial number t of balls. Perhaps surprisingly, Brownian Motions are an essential part of both our proofs.

For p > 1/2, it was known that with probability 1 one of the bins will lead the process at all large enough times. We show that if the first bin starts with 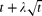balls (for constant λ∈ℝ), the probability that it always or eventually leads has a non-trivial limit depending on λ.

For p ≤ 1/2, it was known that with probability 1 the bins will alternate in leadership. We show, however, that if the initial fraction of balls in one of the bins is > 1/2, the time until it is overtaken by the remaining bin scales like Θ(t1+1/(1-2p)) for p < 1/2 and exp(Θ(t)) for p = 1/2. In fact, the overtaking time has a non-trivial distribution around the scaling factor, which we determine explicitly.

Our proofs use a continuous-time embedding of the balls-in-bins process (due to Rubin) and a non-standard approximation of the process by Brownian Motion. The techniques presented also extend to more general functions f.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 17 , Issue 1 , January 2008 , pp. 87 - 110
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Albert, R. and Barabási, A.-L. (2002) Statistical mechanics of complex networks. Reviews of Modern Physics 74 47–97. Available at arXiv: cond-mat/0106096.CrossRefGoogle Scholar
[2]Alon, N. and Spencer, J. (2000) The Probabilistic Method, 2nd edn, Wiley-Interscience Series in Discrete Mathematics, Wiley, New York.CrossRefGoogle Scholar
[3]Billingsley, P. (1999) Convergence of Probability Measures, 2nd edn, Wiley Series in Probability and Statistics, Wiley, New York.CrossRefGoogle Scholar
[4]Davis, B. (1990) Reinforced random walk. Probab. Theory Rel. Fields 84 203–229.CrossRefGoogle Scholar
[5]Drinea, E., Enachescu, M., and Mitzenmacher, M. (2001) Variations on random graph models of the web. Harvard Technical Report TR-06-01.Google Scholar
[6]Drinea, E., Frieze, A., and Mitzenmacher, M. (2002) Balls in bins processes with feedback. In Proc. 11th Annual ACM-SIAM Symposium on Discrete Algorithms, SIAM, Philadelphia, PA, USA, pp. 308–315.Google Scholar
[7]Khanin, K. and Khanin, R. (2001) A probabilistic model for the establishment of neuron polarity. J. Math. Biology 42 26–40.CrossRefGoogle ScholarPubMed
[8]Krapivsky, P. L. and Redner, S. L. (2001) Organization of growing random networks. Phys. Rev. E 63 066123. Available at arXiv: cond-mat/0011094.CrossRefGoogle ScholarPubMed
[9]Mitzenmacher, M., Oliveira, R., and Spencer, J. (2004) A scaling result for explosive processes. Electron. J. Combin. 11 R31.CrossRefGoogle Scholar
[10]Oliveira, R. (2004) Preferential attachment. PhD thesis, Department of Mathematics, Courant Institute of Mathematical Sciences, New York University.Google Scholar
[11]Oliveira, R. (2005) The onset of dominance in balls-in-bins processes with feedback. Random Struct. Alg., to appear. Available at arXiv: math.PR/0510415.Google Scholar
[12]Oliveira, R. and Spencer, J. (2005) Avoiding an imminent defeat in a balls-in-bins process with feedback. Manuscript.Google Scholar
[13]Spencer, J. and Wormald, N. Explosive processes. Manuscript.Google Scholar