Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-15T09:19:00.505Z Has data issue: false hasContentIssue false
  • English
  • Français

Salt Diffusion Through a Bentonite-Polymer Composite

Published online by Cambridge University Press:  01 January 2024

Gretchen L. Bohnhoff  and
Charles D. Shackelford
Gretchen L. Bohnhoff
Affiliation:
Department of Civil & Environmental Engineering, University of Wisconsin-Platteville, Platteville, Wisconsin 53818-3099, USA
Charles D. Shackelford*
Affiliation:
Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, Colorado 80523-1372, USA
*
*E-mail address of corresponding author: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Bentonites are commonly used as chemical containment barriers to minimize liquid flow and contaminant transport. However, chemicals can adversely affect bentonite performance to the extent that modified bentonites have been developed to improve chemical resistance relative to traditional (unmodified) bentonites. The present study focused on the diffusion of potassium chloride (KCl) through a bentonite-polymer composite, or BPC, that was known to behave as a semipermeable membrane. Specifically, the effective diffusion coefficients, D*, for chloride (Cl−) and potassium (K+) were measured and correlated with previously measured membrane efficiency coefficients, ω, for the BPC. The values of D* at steady-state for chloride (Dss,Cl−*\$\end{document}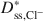) and potassium (Dss,K+*\$\end{document}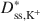) decreased as the ω values increased. The decrease in Dss,Cl−*\$\end{document} 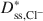and Dss,K+*\$\end{document} 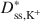was approximately a linear function of (1 − ω), which is consistent with previous research performed on unmodified Na-bentonite contained within a geosynthetic clay liner (GCL). In contrast to the previous GCL tests, however, Dss,Cl−*\$\end{document} 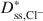values for the BPC generally were greater than the Dss,K+*\$\end{document} 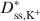values, and the differences between Dss,Cl−*\$\end{document} 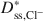and Dss,K+*\$\end{document} 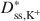decreased as KCl concentration increased. The apparent discrepancy between Dss,Cl−*\$\end{document} 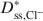and Dss,K+*\$\end{document} 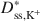is consistent with excess sodium (Na+) in the BPC prior to testing and the requirement for electroneutrality during testing. Also, despite an apparent linear trend in diffusive mass flux for K+, lack of agreement between the ratio of the diffusive mass flux of K+ relative to that for Cl− as required on the basis of electroneutrality at steady state suggested that steadystate diffusive mass flux for K+ had probably not been achieved due to continual K+-for-Na+ cation exchange. Nonetheless, the excess Na+ and bentonite modification did not affect the fundamental correlation between D* and ω, which requires that D* approaches zero as ω approaches unity (D* → 0 as ω → 1).

Keywords

Chemico-osmosisClay MembranesDiffusionElectroneutralityGeosynthetic Clay LinerPolymer-modified BentonitesSemipermeable Membrane BehaviorSodium Bentonite
Type
Research Article
Information
Clays and Clay Minerals , Volume 63 , Issue 3 , June 2015 , pp. 145 - 162
Copyright
Copyright © Clay Minerals Society 2015

References

Ashmawy, A. Darwish, E. Sotelo, N. and Muhammad, N., 2002 Hydraulic performance of untreated and polymer-treated bentonite in inorganic landfill leachates Clays and Clay Minerals 50 546–552.CrossRefGoogle Scholar
Boels, D. and van der Wal, K. (1999) Trisoplast: New developments in soil protection. Sardinia 99, CISA, Caligari, Italy, pp. 77–84.Google Scholar
Bohnhoff, G. (2012) Membrane behavior, diffusion, and compatibility of a polymerized bentonite for containment barrier applications. PhD dissertation, Colorado State University, Fort Collins, Colorado, USA.Google Scholar
Bohnhoff, G. and Shackelford, C., 2013 Improving membrane performance via bentonite polymer nanocomposite Applied Clay Science 86 83–98.CrossRefGoogle Scholar
Christman, M. Benson, C. and Edil, T., 2002 Geophysical evaluation of annular well seals Ground Water Monitoring and Remediation 22 104–112.CrossRefGoogle Scholar
Crank, J., 1975 The Mathematics of Diffusion 2nd edition Oxford, England Clarendon Press.Google Scholar
Di Emidio, G. (2010) Hydraulic and chemico-osmotic performance of polymer treated clay. PhD dissertation, University of Ghent, Belgium.Google Scholar
Di Emidio, G. van Impe, P. and Mazzieri, F., 2010 A polymer enhanced clay for impermeable geosynthetic clay liners Sixth International Conference on Environmental Geotechnics New Delhi, India Tata McGraw Hill 963–967.Google Scholar
Di Emidio, G. van Impe, P. Flores, V., Han, J. and Alzamora, D., 2011 Advances in geosynthetic clay liners: polymer enhanced clays Geo- Frontiers 2011: Advances in Geotechnical Engineering Reston, Virginia, USA ASCE 1931–1940.CrossRefGoogle Scholar
Dominijanni, A. and Manassero, M., 2012 Modelling the swelling and osmotic properties of clay soils. Part I: The phenomenological approach International Journal of Engineering Science 51 32–50.CrossRefGoogle Scholar
Dominijanni, A. and Manassero, M., 2012 Modelling the swelling and osmotic properties of clay soils. Part II: The physical approach International Journal of Engineering Science 51 51–73.CrossRefGoogle Scholar
Dominijanni, A. Manassero, M. and Puma, S., 2013 Coupled chemical-hydraulic-mechanical behaviour of bentonites Geotechnique 63 191–205.CrossRefGoogle Scholar
Estornell, P. and Daniel, D.E., 1992 Hydraulic conductivity of three geosynthetic clay liners Journal of Geotechnical Engineering 118 1592–1606.CrossRefGoogle Scholar
Evans, J., Daniel, D.E. and Trautwein, S., 1994 Hydraulic conductivity of vertical cutoff walls Hydraulic Conductivity and Waste Contaminant Transport in Soil West Conshohocken, Pennsylvania, USA ASTM.Google Scholar
Gleason, M. Daniel, D. and Eykholt, G., 1997 Calcium and sodium bentonite for hydraulic containment applications Journal of Geotechnical and Geoenvironmental Engineering 123 438–445.CrossRefGoogle Scholar
Heller, H. and Keren, R., 2003 Anionic polyacrylamide polymer adsorption by pyrophyllite and montmorillonite Clays and Clay Minerals 51 334–339.CrossRefGoogle Scholar
Jo, H. Benson, C. Shackelford, C. Lee, J.-M. and Edil, T., 2005 Long-term hydraulic conductivity of a geosynthetic clay liner permeated with inorganic salt solutions Journal of Geotechnical and Geoenvironmental Engineering 131 405–417.CrossRefGoogle Scholar
Kajita, L., 1997 An improved contaminant resistant clay for environmental clay liner applications Clays and Clay Minerals 45 609–617.CrossRefGoogle Scholar
Kang, J. and Shackelford, C., 2009 Clay membrane testing using a flexible-wall cell under closed-system boundary conditions Applied Clay Science 44 43–58.CrossRefGoogle Scholar
Kang, J. and Shackelford, C., 2011 Consolidation enhanced membrane behavior of a geosynthetic clay liner Geotextiles and Geomembranes 29 544–556.CrossRefGoogle Scholar
Kolstad, D. Benson, C. and Edil, T., 2004 Hydraulic conductivity and swell of non-prehydrated geosynthetic clay liners permeated with multispecies inorganic solutions Journal of Geotechnical and Geoenvironmental Engineering 130 1236–1249.CrossRefGoogle Scholar
Lagaly, G. Ogawa, M. Dékány, I., Bergaya, F. Theng, B.K.G. and Lagaly, G., 2006 Clay mineral organic interactions Handbook of Clay Science Amsterdam Elsevier.Google Scholar
Malusis, M. and Shackelford, C., 2002 Chemico-osmotic efficiency of a geosynthetic clay liner Journal of Geotechnical and Geoenvironmental Engineering 128 97–106.CrossRefGoogle Scholar
Malusis, M. and Shackelford, C., 2002 Coupling effects during steady-state solute diffusion through a semipermeable clay membrane Environmental Science & Technology 36 1312–1319.CrossRefGoogle ScholarPubMed
Malusis, M. Shackelford, C. and Olsen, H., 2001 A laboratory apparatus to measure chemico-osmotic efficiency coefficients for clay soils Geotechnical Testing Journal 24 229–242.Google Scholar
Manassero, M. and Dominijanni, A., 2003 Modelling the osmosis effect on solute migration through porous media Geotechnique 53 481–492.CrossRefGoogle Scholar
Malusis, M. Kang, J. Shackelford, C., Manassero, M. Dominijanni, A. Foti, S. and Musso, G., 2013 Influence of membrane behavior on solute diffusion through GCLs Coupled Phenomena in Environmental Geotechnics London CRC Press/Balkema, Taylor & Francis Group.Google Scholar
Malusis, M. Kang, J. and Shackelford, C., 2014 Restricted salt diffusion in a geosynthetic clay liner Environmental Geotechnics 2 68–77.CrossRefGoogle Scholar
Mazzieri, F., Han, J. and Alzamora, D., 2011 Impact of desiccation and cation exchange on the hydraulic conductivity of factory-prehydrated GCLs GeoFrontiers 2011: Advances in Geotechnical Engineering Reston, Virginia, USA ASCE.Google Scholar
Mazzieri, F. Di Emidio, G. and Van Impe, P., 2010 Diffusion of calcium chloride in a modified bentonite: impact on osmotic efficiency and hydraulic conductivity Clays and Clay Minerals 58 351–363.CrossRefGoogle Scholar
Mazzieri, F. Pasqualini, E. and Di Emidio, G., 2010 Migration of heavy metals through conventional and factory-prehydrated GCL materials Sixth International Conference on Environmental Geotechnics New Delhi, India Tata McGraw Hill.Google Scholar
Muzny, C. Butler, B. Hanley, H. Tsvetkov, F. and Peiffer, D., 1996 Clay platelet dispersion in a polymer matrix Materials Letters 28 379–384.CrossRefGoogle Scholar
Onikata, M. Kondo, M. Kamon, M., Kamon, M., 1996 Development and characterization of a multiswellable bentonite 2nd International Congress on Environmental Geotechnics Rotterdam, The Netherlands A.A. Balkema.Google Scholar
Onikata, M. Kondo, M. Hayashi, N. and Yamanaka, S., 1999 Complex formation of cation-exchanged montmorillonites with propylene carbonate: Osmotic swelling in aqueous electrolyte solutions Clays and Clay Minerals 47 672–677.CrossRefGoogle Scholar
Scalia, J. (2012) Bentonite-polymer composites for containment applications. PhD dissertation, University of Wisconsin-Madison, Madison, Wisconsin, USA.Google Scholar
Scalia, J. Benson, C. Edil, T. Bohnhoff, G. Shackelford, C., Han, J. and Alzamora, D., 2011 Geosynthetic clay liners containing bentonite polymer nanocomposite GeoFrontiers 2011: Advances in Geotechnical Engineering Reston, Virginia, USA ASCE.Google Scholar
Scalia, Joseph Benson, Craig H. Bohnhoff, Gretchen L. Edil, Tuncer B. and Shackelford, Charles D., 2014 Long-Term Hydraulic Conductivity of a Bentonite-Polymer Composite Permeated with Aggressive Inorganic Solutions Journal of Geotechnical and Geoenvironmental Engineering 140 3 04013025.CrossRefGoogle Scholar
Shackelford, C., 1991 Laboratory diffusion testing for waste disposal — A review Journal of Contaminant Hydrology 7 177–217.CrossRefGoogle Scholar
Shackelford, C., Han, J. and Alzamora, D., 2011 Membrane behavior in geosynthetic clay liners GeoFrontiers 2011: Advances in Geotechnical Engineering Reston, Virginia, USA ASCE.Google Scholar
Shackelford, C., Hryciw, R. Athanasopoulos-Zekkos, A. and Yesiller, N., 2012 Membrane behavior of engineered clay barriers for geoenvironmental containment: State of the art GeoCongress 2012—State of the Art and Practice in Geotechnical Engineering Reston, Virginia, USA ASCE.Google Scholar
Shackelford, C., Manassero, M. Dominijanni, A. Foti, S. and Musso, G., 2013 Membrane behavior in engineered bentonite-based containment barriers: State of the art Coupled Phenomena in Environmental Geotechnics London CRC Press/Balkema, Taylor & Francis Group.Google Scholar
Shackelford, C. Benson, C. Katsumi, T. Edil, T. and Lin, L., 2000 Evaluating the hydraulic conductivity of GCLs permeated with non-standard liquids Geotextiles and Geomembranes 18 133–161.CrossRefGoogle Scholar
Shackelford, C. and Daniel, D., 1991 Diffusion in saturated soil. 1. Background Journal of Geotechnical Engineering 117 467–484.CrossRefGoogle Scholar
Shackelford, C. and Lee, J., 2003 The destructive role of diffusion on clay membrane behavior Clays and Clay Minerals 51 186–196.CrossRefGoogle Scholar
Shackelford, C. and Moore, S., 2013 Fickian diffusion of radionuclides for engineered containment barriers: Diffusion coefficients, porosities, and complicating issues Engineering Geology 152 133–147.CrossRefGoogle Scholar
Shackelford, C. Sample-Lord, K., Iskander, M. Garlanger, J. and Hussein, M., 2014 Hydraulic conductivity and compatibility of bentonite for hydraulic containment applications From Soil Behavior Fundamentals to Innovations in Geotechnical Engineering Reston, Virginia, USA ASCE.Google Scholar
Shackelford, C. Malusis, M. Olsen, H., Culligan, P. Einstein, H. and Whittle, A., 2003 Clay membrane behavior for geoenvironmental containment Soil and Rock America Conference 2003, vol. 1 Essen, Germany Verlag Glückauf GMBH.Google Scholar
Skagius, K. and Neretnieks, I., 1986 Porosities and diffusivities of some non-sorbing species in crystalline rocks Water Resources Research 22 389–398.CrossRefGoogle Scholar
Smith, J. Bartelt-Hunt, S. and Burns, S., 2003 Sorption and permeability of gasoline hydrocarbons in organobentonite porous media Journal of Hazardous Materials 96 91–97.CrossRefGoogle ScholarPubMed
Trauger, R. and Darlington, J. (2000) Next generation geosynthetic clay liners for improved durability and performance. 14th GRI Conference, Geosynthetic Institute, Folsom, Pennsylvania, USA, pp. 255–267.Google Scholar