Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-18T04:26:12.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Extraction of diagenetic and detrital ages and of the 40Kdetrital/40Kdiagenetic ratio from K-Ar dates of clay fractions

Published online by Cambridge University Press:  01 January 2024

Marek Szczerba  and
Jan Środoń
Marek Szczerba*
Affiliation:
Institute of Geological Sciences Polskiej Akademii Nauk, Senacka 1, 31-002 Kraków, Poland
Jan Środoń
Affiliation:
Institute of Geological Sciences Polskiej Akademii Nauk, Senacka 1, 31-002 Kraków, Poland
*
* E-mail address of corresponding author: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Illite age analysis (IAA) is a classical method for extracting diagenetic and detrital ages from mixed ages measured by K-Ar. This approach is based on measuring the masses of diagenetic and detrital illitic components in a few different grain-size fractions of one rock sample and measuring the mixed ages of these fractions. The 1Md illitic polytype is usually considered to be diagenetic, while 2M1 is considered detrital. A plot of the function: exp(λt)−1 (where t is time and λ is the decay constant) vs. weight percent of the detrital fraction is constructed. On the basis of linear extrapolation to end-member fractions, the diagenetic and the detrital age is obtained. This approach does not take into account various K contents in different polytypes (%Kdetrital and %Kdiagenetic). In order to do that, the detrital mass fraction (wt.%detrital) should be recalculated into the percentage of detrital K (%Id(K)):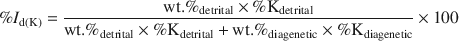

Analytical constraint of the K content of different polytypes is very difficult, so a new approach to this problem has been developed. In the present study, the plot of 40Ar*/40K vs. %Id(K) for a precisely determined ratio of 40Kdetrital/40Kdiagenetic was observed to be linear. On the basis of this observation, a computer program, MODELAGE, was written in the Java programming language using as input a few measured detrital illite mass fractions along with the mixed K-Ar ages of the relevant grain fractions. It then calculates the end-member ages and the 40Kdetrital/40Kdiagenetic ratio using genetic algorithms.

The errors in diagenetic and detrital illite mass-fraction determination mean that the 40Kdetrital/40Kdiagenetic ratio and the end-member ages can be evaluated only with some uncertainty. The best results are obtained if the measured mass fractions represent a relatively broad range. Constraining one of the unknowns (particularly the 40Kdetrital/40Kdiagenetic ratio) improves the results significantly.

Evaluation of data obtained from the literature using the proposed approach leads to the conclusion that the 40Kdetrital/40Kdiagenetic ratio is often >1.00, and some of 1Md illite polytype materials may be of detrital origin. If this is not the case, if a broad range of mass fractions is covered, and if the differences between end-member ages are relatively small, IAA analysis still gives appropriate results, even if the true 40Kdetrital/40Kdiagenetic ratio is different from 1.00.

Keywords

Diagenetic AgeGenetic AlgorithmsIllite Age AnalysisK-ArMixed Ages
Type
Article
Information
Clays and Clay Minerals , Volume 57 , Issue 1 , February 2009 , pp. 93 - 103
Copyright
Copyright © The Clay Minerals Society 2009

References

Bechtel, A. Elliott, W.C. Wampler, J.M. and Oszczepalski, S., 1999 Clay mineralogy, crystallinity, and K/Ar ages of illites in the Polish Zechstein Basin: Implications for the age of the Kupferschiefer-type mineralization Economic Geology 94 261–272 10.2113/gsecongeo.94.2.261.CrossRefGoogle Scholar
Clauer, N. Środoń, J. Franců, J. and Šucha, V., 1997 K-Ar dating of illite fundamental particles separated from illite smectite Clay Minerals 2 233–254.Google Scholar
Dong, H. Hall, C.M. Peacor, D.R. Halliday, A.N. and Pevear, D.R., 2000 Thermal 40Ar/39Ar separation of diagenetic from detrital illitic clays in Gulf Coast shales Earth and Planetary Science Letters 175 309–325 10.1016/S0012-821X(99)00294-0.CrossRefGoogle Scholar
Elliott, W.C. Basu, A. Wampler, J.M. Elmore, R.D. and Grathoff, G.H., 2006 Comparison of K-Ar ages of diagenetic illite-smectite to the age of a chemical remanent magnetization (CRM): an example from the isle of Skye, Scotland Clays and Clay Minerals 54 314–323 10.1346/CCMN.2006.0540303.CrossRefGoogle Scholar
Fergusson, C.L. and Phillips, D., 2001 40Ar/39Ar and K-Ar age constraints on the timing of regional deformation, south coast of New South Wales, Lachlan Fold Belt: problems and implications Australian Journal of Earth Sciences 48 395–408 10.1046/j.1440-0952.2001.00866.x.CrossRefGoogle Scholar
Górecka-Nowak, A., 2008 New interpretations of the Carboniferous stratigraphy of SW Poland based on miospore data Bulletin of Geosciences 83 1–16.Google Scholar
Grathoff, G.H. and Moore, D.M., 1996 Illite polytype quantification using WILDFIRE©-calculated patterns Clays and Clay Minerals 44 835–842 10.1346/CCMN.1996.0440615.CrossRefGoogle Scholar
Grathoff, G.H. Moore, D.M. Hay, R.L. Wemmer, K. et al. , and and Schieber, J. 1998 et al. , Illite polytype quantification in Paleozoic shales: A technique to quantify diagenetic and detrital illite Shale and Mudstones II. Petrography, Petrophysics, Geochemistry, and Economic Geology Stuttgart, Germany Schweizerbart’sche Verlagsbuchhandlung 161–178.Google Scholar
Hower, J. Hurley, P.M. Pinson, W.H. and Fairbairn, H.W., 1963 The dependance of K-Ar age on the mineralogy of various particle size range in a shale Geochimica et Cosmochimica Acta 27 405–410 10.1016/0016-7037(63)90080-2.CrossRefGoogle Scholar
Jowett, E.C. Pearce, G.W. and Rydzewski, A., 1987 A mid-Triassic paleomagnetic age of the Kupferschiefer mineralization in Poland, based on a revised apparent polar wander path for Europe and Russia Journal of Geophysical Research 92 581–598 10.1029/JB092iB01p00581.CrossRefGoogle Scholar
Kosakowski, P. Markiewicz, A. Kotarba, M.J. Oszczepalski, S. and Wiȩcław, D., 2007 The timing of ore mineralization based on thermal maturity modeling of Kupferschiefer strata and its relation to tectonics of southern part of the Fore-Sudetic Monocline (SW Poland) PGI Bulletin 423 139–150 (in Polish).Google Scholar
Koza, J., 1992 Genetic Programming: On the Programming of Computers by Means of Natural Selection Harvard, Massachusetts, USA MIT Press 819 pp.Google Scholar
Kucha, H. et al. , and and Parnell, J. 1993 et al. , Noble metals associated with organic matter, Kupfershiefer, Poland Bitumens in Ore Deposits Berlin, Germany Springer Verlag 153–170 10.1007/978-3-642-85806-2_10.CrossRefGoogle Scholar
Kucha, H. and Przybyłowicz, W., 1999 Noble metals in organic matter and clay-organic matrices, Kupferschiefer, Poland Economic Geology 94 1137–1162 10.2113/gsecongeo.94.7.1137.CrossRefGoogle Scholar
Lindgreen, H. Drits, V.A. Sakharov, B.A. Salyn, A.L. Wrang, P. and Dainyak, L.G., 2000 Illite-smectite structural changes during metamorphism in black Cambrian Alum shales from the Baltic area American Mineralogist 85 1223–1238 10.2138/am-2000-8-916.CrossRefGoogle Scholar
Mazur, S. Dunlap, W.J. Turniak, K. and Oberc-Dziedzic, T., 2006 Age constraints for thermal evolution and erosional history of the central European Variscan belt: New data from the sediments and basement of the Carboniferous basin in western Poland Journal of the Geological Society 163 1011–1024 10.1144/0016-76492004-170.CrossRefGoogle Scholar
Michalik, M., 2001 Diagenesis of the Weissliegend sandstones in the south-western margin of the Polish Rotliegend Basin Prace Mineralogiczne 91 3–171.Google Scholar
Mossman, J.R. Clauer, N. and Liewig, N., 1992 Dating thermal anomalies in sedimentary basins: the diagenetic history of clay minerals in the Triassic sandstones of the Paris Basin, France Clay Minerals 27 211–226 10.1180/claymin.1992.027.2.06.CrossRefGoogle Scholar
Pevear, D.R., Kharaka, Y.K. and Maest, A.S., 1992 Illite age analysis, a new tool for basin thermal history analysis Water-Rock Interaction Rotterdam, The Netherlands A.A. Balkema 1251–1254.Google Scholar
Pevear, D.R., 1999 Illite and hydrocarbon exploration Proceedings of the National Academy of Sciences of the United States of America 96 3440–3446 10.1073/pnas.96.7.3440.CrossRefGoogle ScholarPubMed
Pokorski, J., 1988 Paleotectonic maps of the Rotliegendes in Poland Geological Quarterly 32 15–32 (in Polish).Google Scholar
Sawłowicz, Z., 1989 Organic matter in the Zechstein Kupferschiefer from the Fore-Sudetic Monocline (Poland). I. Bitumens Mineralogia Polonica 20 69–89.Google Scholar
Schneider, D.A. Zahniser, S.J. Glascock, J.M. Gordon, S.M. and Manecki, M., 2006 Thermochronology of the west Sudetes (Bohemian Massif): Rapid and repeated eduction in the eastern Variscides, Poland and Czech Republic American Journal of Science 306 846–873 10.2475/10.2006.03.CrossRefGoogle Scholar
Sun, Y.-Z., 1998 Influences of secondary oxidation and sulfide formation on several maturity parameters in Kupferschiefer Organic Geochemistry 29 1419–1429 10.1016/S0146-6380(98)00128-4.CrossRefGoogle Scholar
Środoń, J., 1999 Extracting K-Ar ages from shales: a theoretical test Clay Minerals 33 375–378 10.1180/000985599546163.CrossRefGoogle Scholar
Środoń, J., 2000 Reply to discussion of ‘Extracting K-Ar ages from shales: a theoretical test’ Clay Minerals 35 605–608 10.1180/000985500546927.CrossRefGoogle Scholar
Środoń, J. Clauer, N. and Eberl, D.D., 2002 Interpretation of K-Ar dates of illitic clays from sedimentary rocks aided by modeling American Mineralogist 87 1528–1535 10.2138/am-2002-11-1202.CrossRefGoogle Scholar
Turniak, K. Halas, S. and Wójtowicz, A., 2007 New K-Ar cooling ages of granitoids from the Strzegom-Sobótka Massif, SW Poland Geochronomertia 27 5–9 10.2478/v10003-007-0019-9.CrossRefGoogle Scholar
van der Pluijm, B.A. Hall, C.M. Vrolijk, P. Pevear, D.R. and Covey, M., 2001 The dating of shallow faults in the Earth’s crust Nature 412 172–174 10.1038/35084053.CrossRefGoogle ScholarPubMed
Ylagan, R.F. Pevear, D.R. and Vrolijk, P.J., 2000 Discussion of ‘Extracting K-Ar ages from shales: a theoretical test’ Clay Minerals 35 599–604 10.1180/000985500546918.CrossRefGoogle Scholar