Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T11:01:53.351Z Has data issue: false hasContentIssue false
  • English
  • Français

The Zeta Function of a Pair of Quadratic Forms

Published online by Cambridge University Press:  20 November 2018

Laura Mann Schueller
Laura Mann Schueller*
Affiliation:
Department of Mathematics Whitman College Walla Walla, Washington 99362 U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The zeta function of a nonsingular pair of quadratic forms defined over a finite field, 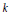$k$, of arbitrary characteristic is calculated. A. Weil made this computation when char 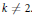$k\,\ne \,2$. When the pair has even order, a relationship between the number of zeros of the pair and the number of places of degree one in an appropriate hyperelliptic function field is established.

Keywords

11G25
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 2 , 01 June 2001 , pp. 242 - 256
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Arf, C., Untersuchungen über quadratische Formen in Körpern der Charakteristic 2. J. Reine Angew. Math. 183 (1941), 148–167.Google Scholar
[2] Ireland, K. and Rosen, M., A Classical Introduction to Modern Number Theory 2nd Ed. Graduate Texts in Math. 84, Springer-Verlag, New York, 1990.Google Scholar
[3] Kneser, M., Vorlesung über quadratische Formen. Göttingen, Math. Institut, 1973–4.Google Scholar
[4] Knus, M., Quadratic Forms, Clifford Algebras and Spinors. Seminars in Mathematics, 1, Campinas, Brazil, 1988.Google Scholar
[5] Lam, T., The Algebraic Theory of Quadratic Forms.Mathematics Lecture Note Series, W. A. Benjamin, Inc., Reading, MA, 1973.Google Scholar
[6] Leep, D. and Schueller, L., Zeros of a Pair of Quadratic Forms Defined Over a Finite Field. Finite Fields Appl. (2) 5 (1999), 157–176.Google Scholar
[7] Leep, D. and Schueller, L., A Characterization of Nonsingular Pairs of Quadratic Forms. submitted, 1998.Google Scholar
[8] Lidl, R. and Niederreiter, H., Finite Fields. Encyclopedia of Math. and its Applications 20, Cambridge Univ. Press, New York, 1984.Google Scholar
[9] Schmidt, W., Equations over finite fields: an elementary approach. LectureNotes inMath. 536, Springer-Verlag, New York, 1976.Google Scholar
[10] Stichtenoth, H., Algebraic Function Fields and Codes. Universitext, Springer-Verlag, Berlin, Heidelberg, 1993.Google Scholar
[11] Weil, A., Footnote to a Recent Paper. Amer. J.Math. 76 (1954), 347–350.Google Scholar
[12] Witt, E., Über eine Invariante quadratischer Formen mod 2. J. Reine Angew. Math. 193 (1954), 119–120.Google Scholar