Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T03:34:40.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Wirtinger's Inequalities on Time Scales

Published online by Cambridge University Press:  20 November 2018

Ravi P. Agarwal ,
Victoria Otero-Espinar ,
Kanishka Perera  and
Dolores R. Vivero
Ravi P. Agarwal
Affiliation:
Department of Mathematical Sciences, Florida Institute of Technology, Melbourne, FL 32901, U.S.A. e-mail: [email protected]
Victoria Otero-Espinar
Affiliation:
Departamento de Análise Matemática, Facultade de Matemáticas, Universidade de Santiago de Compostela, Galicia, Spain e-mail: [email protected] e-mail: [email protected] e-mail: [email protected]
Kanishka Perera
Affiliation:
Departamento de Análise Matemática, Facultade de Matemáticas, Universidade de Santiago de Compostela, Galicia, Spain e-mail: [email protected] e-mail: [email protected] e-mail: [email protected]
Dolores R. Vivero
Affiliation:
Departamento de Análise Matemática, Facultade de Matemáticas, Universidade de Santiago de Compostela, Galicia, Spain e-mail: [email protected] e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

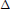This paper is devoted to the study of Wirtinger-type inequalities for the Lebesgue $\Delta$-integral on an arbitrary time scale $\mathbb{T}$. We prove a general inequality for a class of absolutely continuous functions on closed subintervals of an adequate subset of $\mathbb{T}$. By using this expression and by assuming that $\mathbb{T}$ is bounded, we deduce that a general inequality is valid for every absolutely continuous function on $\mathbb{T}$ such that its 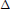$\Delta$-derivative belongs to 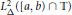$L_{\Delta }^{2}\,([a,\,b)\,\cap \,\mathbb{T})$ and at most it vanishes on the boundary of $\mathbb{T}$.

Keywords

39A10time scales calculusΔ-integralWirtinger's inequality
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 2 , 01 June 2008 , pp. 161 - 171
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Agarwal, R. P., Difference Equations and Inequalities. Theory, Methods, and Applications. Second edition. Monographs and Textbooks in Pure and Applied Mathematics 228. Marcel Dekker, New York, 2000.Google Scholar
[2] Agarwal, R. P., Bohner, M., and Peterson, A., Inequalities on time scales: a survey. Math. Inequal. Appl. 4(2001), no. 4, 535–557.Google Scholar
[3] Agarwal, R. P., Čuljak, V., and Pečarić, J., On discrete and continuousWirtinger inequalities. Appl. Anal. 70(1998), no. 1–2, 195–204.Google Scholar
[4] Agarwal, R. P., Espinar, V. O., Perera, K., and Vivero, D. R., Basic properties of Sobolev's spaces on time scales. Adv. Difference Equ. 2006 Article 38121, 14 pp.Google Scholar
[5] Agarwal, R. P., Espinar, V. O., Perera, K., and Vivero, D. R., Multiple positive solutions of singular Dirichlet problems on time scales via variational methods. Nonlinear Anal. 67(2007), no. 2, 368–381.Google Scholar
[6] Beesack, P. R., Integral inequalities of Wirtinger type. Duke Math. J. 25(1958), 477–498.Google Scholar
[7] Bohner, M. and Peterson, A., Dynamic Equations on Time Scales. An Introduction with Applications. Birkhäuser Boston, Boston, MA, 2001.Google Scholar
[8] Bohner, M. and Peterson, A., eds. Advances in Dynamic Equations on Time Scales. Birkhäuser Boston, Boston, MA, 2003.Google Scholar
[9] Cabada, A. and Vivero, D. R., Expression of the Lebesgu Δ-integral on time scales as a usual Lebesgue integral. Application to the calculus of Δ–antiderivatives. Math. Comput. Modelling 43(2006), no. 1–2, 194–207.Google Scholar
[10] Cabada, A. and Vivero, D. R., Criterions for absolutely continuity on time scales. J. Difference Equ. Appl. 11(2005), no. 11, 1013–1028.Google Scholar
[11] Dautray, R. and Lions, J.-L., Mathematical Analysis and Numerical Methods for Science and Technology. Vol. 2. Functional and Variational Methods. Springer-Verlag, Berlin, 1988.Google Scholar
[12] Hardy, G. H., Littlewood, J. E., and Pólya, G., Inequalities. Second edition. Cambridge, at the University Press, 1952.Google Scholar
[13] Hilscher, R., A time scales version of a Wirtinger-type inequality and applications. Dynamic equations on time scales. J. Comput. Appl. Math. 141(2002), no. 1–2, 219–226.Google Scholar
[14] Hilger, S., Ein Maßkettenkalkül mit Anwendung auf Zentrumsmannigfaltigkeiten. Ph.D. thesis, Universität Würzburg, 1988.Google Scholar
[15] Kaymakçalan, B., Lakshmikantham, V., and Sivasundaram, S., Dynamical Systems on Measure Chains. Kluwer, Dordrecht, 1996.Google Scholar
[16] Lee, C.-F., Yeh, C.-C., Hong, C.-H., and Agarwal, R. P., Lyapunov and Wirtinger inequalities. Appl. Math. Lett. 17(2004), no. 7, 847–853.Google Scholar
[17] Milovanović, G. V. and Milovanović, I. Z., Discrete inequalities of Wirtinger's type. In: Recent Progress in Inequalities. Math. Appl. 430, Kluwer, Dordrecht, 1998, pp. 289–308.Google Scholar
[18] Mawhin, J. and Willem, M., Critical Point Theory and Hamiltonian Systems. Applied Mathematical Sciences 74. Springer-Verlag, New York, 1989.Google Scholar
[19] Swanson, C. A., Wirtinger's inequality. SIAM J. Math. Anal. 9(1978), no. 3, 484–491.Google Scholar