Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T19:40:05.279Z Has data issue: false hasContentIssue false
  • English
  • Français

Which Rationals are Ratios of Pisot Sequences?

Published online by Cambridge University Press:  20 November 2018

David Boyd
David Boyd*
Affiliation:
Department of mathematics, University of British ColumbiaVancouver, B.C., CanadaV6T 1Y4
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A Pisot sequence is a sequence of integers defined recursively by the formula - 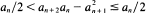. If 0 < a0 < a1 then an+1/an converges to a limit θ. We ask whether any rational p/q other than an integer can ever occur as such a limit. For p/q > q/2, the answer is no. However, if p/q < q/2 then the question is shown to be equivalent to a stopping time problem related to the notorious 3x + 1 problem and to a question of Mahler concerning the powers of 3/2. Although some interesting statistical properties of these stopping time problems can be established, we are forced to conclude that the question raised in the title of this paper is perhaps more intractable than it might appear.

Keywords

10F4010L1012A15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 28 , Issue 3 , 01 September 1985 , pp. 343 - 349
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Boyd, D.W., Pisot sequences which satisfy no linear recurrence, Acta Arith. 32 (1977), pp. 89—98 Google Scholar
2. Boyd, D.W., On linear recurrence relations satisfied by Pisot sequences, to appear.Google Scholar
3. Conway, J.H., Unpredictable iterations, Proc. 1972 Number Theory Conference, Boulder, Colo., pp. 49–52, MR53 #13717.Google Scholar
4. Everett, C.J., Iteration of the number theoretic function f(2n) = n,f(2n + 1) = 3n + 2, Advances in Math. 25 (1977), pp. 42–45.Google Scholar
5. Flor, P., Uber eine Klasse von Folgen naturlicher Zahlen, Math. Annalen 140 (1960), pp. 299—307 Google Scholar
6. Gantmacher, F.R., The Theory of Matrices, Chelsea Publishing Co., N.Y., 1971.Google Scholar
7. Katok, A.B., Sinai, Ya.G. and Stepin, A.M., Theory of dynamical systems and general transformation groups with invariant measure, Jour. Soviet Math. 7 (1977), pp. 974—1065 Google Scholar
8. Kemeny, J.G., Snell, J.L. and Knapp, A.W., Denumerable Markov Chains, Springer-Verlag, 1976.Google Scholar
9. Lagarias, J.C., The 3x + 1 problem and its generalizations, Amer. Math. Monthly, 92 (1985), pp. 3–23.Google Scholar
10. Mahler, K., An unsolved problem on the powers of 3/2, Jour. Australian Math. Soc. 8 (1968), pp. 313–321.Google Scholar
11. Pisot, Ch., La répartition modulo 1 et les nombres algébriques, Ann. Scuola Norm. Sup. Pisa 7 (1938), pp. 205–248.Google Scholar
12. Terras, R., A stopping time problem on the positive integers, Acta Arith. 30 (1976), pp. 241–252.Google Scholar