Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T19:16:29.020Z Has data issue: false hasContentIssue false
  • English
  • Français

Well-posedness of Third Order Differential Equations in Hölder Continuous Function Spaces

Part of: General theory of linear operators Differential equations in abstract spaces Functional-differential and differential-difference equations Groups and semigroups of linear operators, their generalizations and applications

Published online by Cambridge University Press:  15 October 2018

Shangquan Bu  and
Gang Cai
Shangquan Bu
Affiliation:
Department of Mathematical Science, University of Tsinghua, Beijing 100084, China Email: [email protected]
Gang Cai
Affiliation:
School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, China Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, by using operator-valued 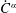${\dot{C}}^{\unicode[STIX]{x1D6FC}}$-Fourier multiplier results on vector-valued Hölder continuous function spaces, we give a characterization of the 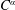$C^{\unicode[STIX]{x1D6FC}}$-well-posedness for the third order differential equations 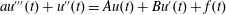$au^{\prime \prime \prime }(t)+u^{\prime \prime }(t)=Au(t)+Bu^{\prime }(t)+f(t)$, (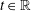$t\in \mathbb{R}$), where 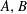$A,B$ are closed linear operators on a Banach space 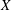$X$ such that 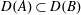$D(A)\subset D(B)$, 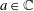$a\in \mathbb{C}$ and 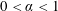$0<\unicode[STIX]{x1D6FC}<1$.

Keywords

C𝛼 -well-posednessdegenerate differential equationĊ𝛼 -Fourier multiplierHölder continuous function space

MSC classification

Primary: 34G10: Linear equations
Secondary: 47D06: One-parameter semigroups and linear evolution equations 47A10: Spectrum, resolvent 34K30: Equations in abstract spaces
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 4 , December 2019 , pp. 715 - 726
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This work was supported by the NSF of China (Grants No. 11571194, 11731010, 11771063), the Natural Science Foundation of Chongqing (cstc2017jcyjAX0006, cstc2016jcyjA0116), Science and Technology Project of Chongqing Education Committee (Grants No. KJ1703041, KJZDM201800501, KJ16003162016), the University Young Core Teacher Foundation of Chongqing (020603011714), Talent Project of Chongqing Normal University (Grant No. 02030307-00024). Gang Cai is corresponding author.

References

Arendt, W., Batty, Ch., and Bu, S., Fourier multipliers for Hölder continuous functions and maximal regularity . Studia Math. 160(2004), 23–51.Google Scholar
Arendt, W., Batty, Ch., Hieber, M., and Neubrander, F., Vector-valued Laplace Transforms and Cauchy Problems . Birkhäuser, Basel, 2001.Google Scholar
Bose, S. K. and Gorain, G. C., Exact controllability and boundary stabilization of torsional vibrations of an internally damped flexible space structure . J. Optim. Theory Appl. 99(1998), 423–442.Google Scholar
Bose, S. K. and Gorain, G. C., Exact controllability and boundary stabilization of flexural vibrations of an internally damped flexible space structure . Appl. Math. Comput. 126(2002), 341–360.Google Scholar
Bu, S., Well-posedness of degenerate differential equations in Hölder continuous function spaces . Front. Math. China 10(2015), no. 2, 239–248.Google Scholar
Bu, S. and Cai, G., Well-posedness of second order degenerate differential equations in Hölder continuous function spaces . Expo. Math. 34(2016), no. 2, 223–236.Google Scholar
Gorain, G. C., Boundary stabilization of nonlinear vibrations of a flexible structure in a bounded domain in ℝ n . J. Math. Anal. Appl. 319(2006), 635–650.Google Scholar
Haase, M., The Functional Calculus for Sectorial Operators . Birkhäuser Verlag, Basel, 2005.Google Scholar
Kalton, N. and Weis, L., The H ∞ -calculus and sums of closed operators . Math. Ann. 321(2001), 319–345.Google Scholar
Keyantuo, V. and Lizama, C., Hölder continuous solutions for integro-differential equations and maximal regularity . J. Differential Equations 230(2006), 634–660.Google Scholar
Marchand, R., McDevitt, T., and Triggiani, R., An abstract semigroup approach to the third-order Moore–Gibson–Thompson partial differential equation arising in high- intensity ultrasound: structural decomposition, spectral analysis, exponential stability . Math. Methods Appl. Sci. 35(2012), no. 15, 1896–1929.Google Scholar
Poblete, V. and Pozo, J. C., Periodic solutions of an abstract third-order differential equation . Studia Math. 215(2013), 195–219.Google Scholar
Ponce, R., Hölder continuous solutions for Sobolev type differential equations . Math. Nachr. 287(2014), no. 1, 70–78.Google Scholar
Ponce, R., On the well-posedness of degenerate fractional differential equations in vector valued function spaces . Israel J. Math. 219(2017), 727–755.Google Scholar