Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T16:30:10.265Z Has data issue: false hasContentIssue false
  • English
  • Français

The Waring Problem with the Ramanujan τ -Function, II

Published online by Cambridge University Press:  20 November 2018

M. Z. Garaev ,
V. C. Garcia  and
S. V. Konyagin
M. Z. Garaev
Affiliation:
Instituto de Matemáticas, Universidad Nacional Autónoma de México, C.P. 58089, Morelia, Michoacán, México e-mail: [email protected]@matmor.unam.mx
V. C. Garcia
Affiliation:
Instituto de Matemáticas, Universidad Nacional Autónoma de México, C.P. 58089, Morelia, Michoacán, México e-mail: [email protected]@matmor.unam.mx
S. V. Konyagin
Affiliation:
Department of Mechanics and Mathematics, Moscow State University, Moscow, 119992, Russia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 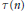$\tau \left( n \right)$ be the Ramanujan $\text{ }\!\!\tau\!\!\text{ }$-function. We prove that for any integer 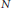$N$ with 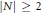$\left| N \right|\,\ge \,2$ the diophantine equation

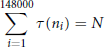$$\underset{i=1}{\overset{148000}{\mathop{\sum }}}\,\,\tau \left( {{n}_{i}} \right)\,=\,N$$

has a solution in positive integers 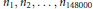${{n}_{1}},\,{{n}_{2}},\,.\,.\,.\,,\,{{n}_{148000}}$ satisfying the condition

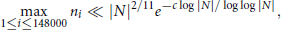$$\underset{1\le i\le 148000}{\mathop{\max }}\,{{n}_{i}}\ll |N{{|}^{2/11}}{{e}^{-c\log |N|/\log \log |N|}},$$

for some absolute constant 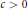$c\,>\,0$.

Keywords

11B1311F30
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 2 , 01 June 2009 , pp. 195 - 199
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Apostol, T. M., Modular functions and Dirichlet series in number theory. Second ed., Graduate Texts in Mathematics 41, Springer-Verlag, New York, 1990.Google Scholar
[2] Bourgain, J., Katz, N., and Tao, T., A sum-product estimate in finite fields and their applications. Geom. Funct. Anal. 14(2004), no. 1, 27–57.Google Scholar
[3] Deligne, P., La conjecture de Weil. I. Inst. Hautes Études Sci. Publ. Math. 43(1974), 273–307.Google Scholar
[4] Garaev, M. Z., Garcia, V. C., and Konyagin, S. V.,Waring problem with the Ramanujan τ-function. Izvestiya: Mathematics 72(2008), no. 1, 35–46.Google Scholar
[5] Hua, L.-K., The additive prime number theory. Trav. Inst. Math. Stekloff 22(1947).Google Scholar
[6] Iwaniec, H., Topics in clasical automorphic forms. Graduate Studies inMathematics 17, American Mathematical Society, Providence, Rhode Island, 1997.Google Scholar
[7] Koblitz, N., Introduction to elliptic curves and modular forms Second ed., Springer-Verlag, New York, 1993.Google Scholar
[8] Murty, M. R., Oscillations of Fourier coefficients of modular forms. Math. Ann. 262(1983), no. 4, 431–446.Google Scholar
[9] Niebur, D., A formula for Ramanujan's τ-function. Illinois J. Math. 19(1975), 448–449.Google Scholar
[10] Serre, J.-P., Congruences et formes modulaires. Lecture Notes in Math. 317, Springer, Berlin, 1973, 319–338.Google Scholar
[11] Shparlinski, I. E., On the value set of the Ramanujan function. Arch. Math. 85(2005), no. 6, 508–513.Google Scholar