Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T15:13:00.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Variations on Müntz's Theme

Published online by Cambridge University Press:  20 November 2018

Peter B. Borwein
Peter B. Borwein*
Affiliation:
Department of Mathematics, Dalhousie University, Halifax, Nova Scotia B3H 4H8
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

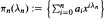We consider some variations of Muntz's classical theorem on when Span{xλi} is dense in C[0,1]. We prove, for example, that if then the collection of spaces 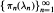is dense in C[0,1] if and only if lim sup(log 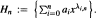n)/λn = ∞. Another variation concerns the denseness of the union of spaces of the form The derivations of these results require an examination of the location of the zeros of the associated Chebyshev polynomials.

Keywords

41A50Miintz TheoremMarkov SystemsChebyshev Polynomials
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 34 , Issue 3 , 01 September 1991 , pp. 305 - 310
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Borwein, P. B., Zeros of Chebyshev polynomials in Markov systems, J. Approx. Theory 63 (1990), 56–64.Google Scholar
2. Cheney, E. W., Introduction to approximation theory. McGraw-Hill, New York, 1966.Google Scholar
3. Feinerman, R. P. and Newman, D. J., Polynomial approximation. Williams and Wilkins, Baltimore, Md., 1976.Google Scholar
4. Smith, P. W., An improvement theorem for Descartes systems, Proc. A.M.S. 70 (1978), 26–30.Google Scholar