Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T18:46:46.686Z Has data issue: false hasContentIssue false
  • English
  • Français

Variants of Korselt’s Criterion

Published online by Cambridge University Press:  20 November 2018

Thomas Wright
Thomas Wright*
Affiliation:
Department of Mathematics, Wofford College, Spartanburg, SC 29302, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Under sufficiently strong assumptions about the first term in an arithmetic progression, we prove that for any integer $a$, there are infinitely many 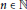$n\,\in \,\mathbb{N}$ such that for each prime factor 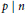$p\,\text{ }\!\!|\!\!\text{ }\,n$, we have 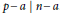$p\,-\,a\,\text{ }\!\!|\!\!\text{ }\,n\,-\,a$. This can be seen as a generalization of Carmichael numbers, which are integers $n$ such that 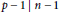$p\,-\,1\,\text{ }\!\!|\!\!\text{ }\,n\,-\,1$ for every 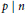$p\,\text{ }\!\!|\!\!\text{ }\,n$.

Keywords

11A51Carmichael numberpseudoprimeKorselt’s Criterion, primes in arithmetic progressions
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 4 , 01 December 2015 , pp. 869 - 876
Copyright
Copyright © Canadian Mathematical Society 2015

References

[AGP] Alford, W. R., Granville, A., and Pomerance, C., There are infinitely many Carmichael numbers. Ann. of Math. (2) 139(1994), no. 3, 703–722. http://dx.doi.Org/10.2307/2118576 Google Scholar
[BP] Banks, W. D. and Pomerance, C., On Carmichael numbers in arithmetic progressions. J. Aust. Math. Soc. 88(2010), no. 3, 313–321. http://dx.doi.Org/10.1017/S1446788710000169 Google Scholar
[Ca] Carmichael, R. D., Note on a new number theory function. Bull. Amer. Math. Soc. 16(1910), no. 5, 232–238. http://dx.doi.Org/10.1090/S0002-9904-1910-01892-9 Google Scholar
[EK] Van Emde Boas, P. and Kruyswijk, D., A combinatorial problem on finite Abelian groups III. Zuivere Wisk. (1969) (Math. Centrum, Amsterdam).Google Scholar
[EPT] Ekstrom, A., Pomerance, C., and Thakur, D. S., Infinitude of elliptic Carmichael numbers. J. Aust. Math. Soc. 92(2012), no. 1, 45–60. http://dx.doi.Org/10.1017/S1446788712000080 Google Scholar
[HB] Heath-Brown, D. R., Almost-primes in arithmetic progressions and short intervals. Math. Proc. Cambridge Philos. Soc. 83(1978), no. 3, 357–375. http://dx.doi.Org/10.1017/S0305004100054657 Google Scholar
[Ko] Korselt, A., Problème chinois. L'intermédinaire des mathématiciens 6(1899), 142–143.Google Scholar
[Ma] Matomâki, K., Carmichael numbers in arithmetic progressions. J. Aust. Math. Soc. 94(2013), no. 2, 268–275. http://dx.doi.Org/10.1017/S1446788712000547 Google Scholar
[Me] Meshulam, R., An uncertainty inequality and zero subsums. Discrete Math. 84(1990), no. 2, 197–200. http://dx.doi.Org/10.1016/0012-365X(90)90375-R Google Scholar
[MV] Montgomery, H. and Vaughan, R., Multiplicative number theory I: Classical theory. Cambridge Studies in Advanced Mathematics, 97, Cambridge University Press, 2007.Google Scholar
[RS] Rosser, J. B. and Schoenfeld, L., Approximate formulas for some functions of prime numbers. Illinois J. Math. 6(1962), 64–94.Google Scholar
[Wr2] Rosser, J. B. and Schoenfeld, L., Infinitely many Carmichael numbers in arithmetic progressions. Bull. Lond. Math. Soc. 45(2013), no. 5, 943–952. http://dx.doi.Org/10.1112/blms/bdtO13 Google Scholar
[Xy] Xylouris, T., Ûber die Linniksche Konstante'. arxiv:0906.2749Google Scholar