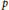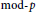Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mináč, Ján
and
Tân, Nguyễn Duy
2016.
Triple Massey products vanish over all fields.
Journal of the London Mathematical Society,
Vol. 94,
Issue. 3,
p.
909.
Mináč, Ján
and
Tân, Nguyễn Duy
2017.
Construction of unipotent Galois extensions and Massey products.
Advances in Mathematics,
Vol. 304,
Issue. ,
p.
1021.
Guillot, Pierre
Mináč, Ján
and
Topaz, Adam
2018.
Four-fold Massey products in Galois cohomology.
Compositio Mathematica,
Vol. 154,
Issue. 9,
p.
1921.
Matzri, Eliyahu
2018.
Triple Massey products of weight (1,n,1) in Galois cohomology.
Journal of Algebra,
Vol. 499,
Issue. ,
p.
272.
Matzri, Eliyahu
2019.
Higher Triple Massey products and symbols.
Journal of Algebra,
Vol. 527,
Issue. ,
p.
136.
Efrat, Ido
2020.
The lower p-central series of a free profinite group and the Shuffle algebra.
Journal of Pure and Applied Algebra,
Vol. 224,
Issue. 6,
p.
106260.