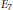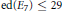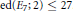Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Garibaldi, Skip
and
Guralnick, Robert M.
2016.
Essential dimension of algebraic groups, including bad characteristic.
Archiv der Mathematik,
Vol. 107,
Issue. 2,
p.
101.
Lötscher, Roland
and
MacDonald, Mark
2017.
The slice method for G-torsors.
Advances in Mathematics,
Vol. 320,
Issue. ,
p.
329.
Pirisi, Roberto
and
Talpo, Mattia
2019.
On the Motivic Class of the Classifying Stack of $G_2$ and the Spin Groups.
International Mathematics Research Notices,
Vol. 2019,
Issue. 10,
p.
3265.