Hostname: page-component-f554764f5-wjqwx Total loading time: 0 Render date: 2025-04-12T12:13:46.592Z Has data issue: false hasContentIssue false
  • English
  • Français

Universal Power Series in ℂN

Published online by Cambridge University Press:  20 November 2018

Raphaël Clouâtre
Raphaël Clouâtre*
Affiliation:
Department of Mathematics, Indiana University, Bloomington, IN 47405, U.S.A.e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We establish the existence of power series in 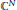${{\mathbb{C}}^{N}}$ with the property that the subsequences of the sequence of partial sums uniformly approach any holomorphic function on any well chosen compact subset outside the set of convergence of the series. We also show that, in a certain sense, most series enjoy this property.

Keywords

32A0532E30
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 2 , 01 June 2011 , pp. 230 - 236
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Chui, C. K. and Parnes, M. N., Approximation by overconvergence of a power series. J. Math. Anal. Appl. 36(1971), 693–696. doi:10.1016/0022-247X(71)90049-7Google Scholar
[2] Grosse-Erdmann, K.-G., Universal families and hypercyclic operators. Bull. Amer. Math. Soc. (N. S.) 36(1999), no. 3, 345–381. doi:10.1090/S0273-0979-99-00788-0Google Scholar
[3] Hörmander, L., An introduction to complex analysis in several variables. D. Van Nostrand Co., Inc., Princeton-Toronto-London, 1966.Google Scholar
[4] Luh, W., Approximation analytischer Funktionen durch überconvergente Potenzreiken und deren Matrix-Transformierten. Mitt. Math. Sem. Giessen 88(1970), 1–56.Google Scholar
[5] Nestoridis, V., Universal Taylor series. Ann. Inst. Fourier (Grenoble) 46(1996), no. 5, 1293–1306.Google Scholar
[6] Nestoridis, V. and Papadimitropoulos, C., Abstract theory of universal series and an application to Dirichlet series. C. R. Math. Acad. Sci. Paris 341(2005), no. 9, 539–543.Google Scholar
[7] Seleznev, A. I., On universal power series. (Russian), Mat. Sbornik N. S. 28(70)(1951), 453–460.Google Scholar