Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T21:44:37.295Z Has data issue: false hasContentIssue false
  • English
  • Français

The Uniform Continuity of Functions in Sobolev Spaces

Published online by Cambridge University Press:  20 November 2018

R. A. Adams
R. A. Adams*
Affiliation:
Department of Mathematics, The University of British Columbia, Vancouver, B.C., Canada V6T 1W5
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Functions in 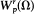, may have to be uniformly continuous on Ω even if Ω is not a Lipschitz domain.

Keywords

46E35
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 19 , Issue 2 , 01 June 1976 , pp. 129 - 136
Copyright
Copyright © Canadian Mathematical Society 1976

Footnotes

(1)

Research partially supported by the National Research Council of Canada under Operating Grant number A-3973.

References

1. Adams, R. A., Soboiev Spaces, Academic Press, New York, 1975.Google Scholar
2. Burenkov, V. I., The approximation of functions in Soboiev spaces by functions of compact support on an arbitrary open set. Dokl. Akad. Nauk CCCP, 202 (1972) 259–262. Engl. Transi. Soviet Math. Dokl. 13 (1972) 60–64.Google Scholar
3. Burenkov, V. I., The approximation of functions in the space for arbitrary open sets Ω by function with compact support. (Russian). Studies in the theory and applications of differentiate functions of several variables, V. Trudy. Mat. Inst. Steklov 131 (1974), 51–63.Google Scholar
4. Gagliardo, E., Proprietà di alcune classi di funzioni in più variabili, Ric. Mat., 7 (1958), 102–137.Google Scholar