Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T10:14:56.667Z Has data issue: false hasContentIssue false
  • English
  • Français

The Uncomplemented Subspace K(X,Y)

Published online by Cambridge University Press:  20 November 2018

Ioana Ghenciu
Ioana Ghenciu*
Affiliation:
University of Wisconsin – River Falls, Department of Mathematics, River Falls, WI 54022–5001 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A vector measure result is used to study the complementation of the space 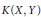$K\left( X,Y \right)$ of compact operators in the spaces 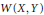$W\left( X,Y \right)$ of weakly compact operators, 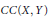$CC\left( X,Y \right)$ of completely continuous operators, and 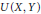$U\left( X,Y \right)$ of unconditionally converging operators. Results of Kalton and Emmanuele concerning the complementation of 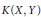$K\left( X,Y \right)$ in 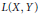$L\left( X,Y \right)$ and in 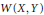$W\left( X,Y \right)$ are generalized. The containment of 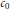${{c}_{0}}$ and 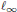${{\ell }_{\infty }}$ in spaces of operators is also studied.

Keywords

46B2046B28compact operatorsweakly compact operatorsuncomplemented subspaces of operators
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 1 , 01 March 2013 , pp. 65 - 69
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Bator, E. and Lewis, P.W., Complemented spaces of operators. Bull. Polish Acad. Sci. Math. 50 ((2002), no. 4, 413–416.Google Scholar
[2] Diestel, J., Sequences and series in Banach spaces. Graduate Texts in Mathematics, 92, Springer-Verlag, Berlin, 1984.Google Scholar
[3] Diestel, J., Jarchow, H., and Tonge, A., Absolutely summing operators. Cambridge Studies in Advanced Mathematics, 43, Cambridge University Press, Cambridge, 1995.Google Scholar
[4] Emmanuele, G., Remarks on the uncomplemented subspaceW(E, F). J Funct Anal 99 ((1991), no. 1, 125–130. http://dx.doi.org/10.1016/0022-1236(91)90055-A Google Scholar
[5] Emmanuele, G., A remark on the containment of c0 in spaces of compact operators. Math. Proc. Cambridge Philos. Soc. 111 ((1992), no. 2, 331–335. http://dx.doi.org/10.1017/S0305004100075435 Google Scholar
[6] Emmanuele, G., About the position of Kw*(X*, Y) inside Lw* (X*, Y). Atti. Sem. Mat. Fis. Univ. Modena 42 ((1994), no. 1, 123–133.Google Scholar
[7] Emmanuele, G. and John, K., Uncomplementability of spaces of compact operators in larger spaces of operators. Czechoslovak Math. J. 47 ((1997), no. 1, 19–32. http://dx.doi.org/10.1023/A:1022483919972 Google Scholar
[8] Feder, M., On subspaces with an unconditional basis and spaces of operators. Illinois J. Math. 24 ((1980), no. 2, 196–205.Google Scholar
[9] Feder, M., On the non-existence of a projection onto the space of compact operators. Canad. Math. Bull.25 ((1982), no. 1, 78–81. http://dx.doi.org/10.4153/CMB-1982-011-0 Google Scholar
[10] Ghenciu, I. and Lewis, P., The embeddability of c0 in spaces of operators. Bull. Pol. Acad. Sci. Math.56 ((2008), no. 3–4, 239–256. http://dx.doi.org/10.4064/ba56-3-7 Google Scholar
[11] John, K., On the uncomplemented subspace K(X,Y). Czechoslovak Math J 42 ((1992), no. 1, 167–173.Google Scholar
[12] Kalton, N. J., Spaces of compact operators. Math. Ann. 208 ((1974), 267–278.http://dx.doi.org/10.1007/BF01432152 Google Scholar
[13] Lewis, P. and Schulle, P., Non-complemented spaces of linear operators, vector measures, and c0. Canad.Math. Bull. Published electronically May 6, 2011. http://dx.doi.org/10.4153/CMB-2011-084-0 Google Scholar
[14] Ruess, W., Duality and geometry of spaces of compact operators. Functional analysis: surveys and recent results, III. (Paderborn,1983). North-Holland Math. Stud., 90, North-Holland, Amsterdam, 1984, pp. 59–78.Google Scholar