Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T11:28:30.541Z Has data issue: false hasContentIssue false
  • English
  • Français

The Uncomplemented Spaces W(X, Y) and K(X, Y)

Published online by Cambridge University Press:  20 November 2018

Paul Lewis
Paul Lewis*
Affiliation:
Department of Mathematics, University of North Texas, Box 311430, Denton, TX 76203-1430, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Classical results of Kalton and techniques of Feder are used to study the complementation of the space 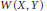$W\left( X,\,Y \right)$ of weakly compact operators and the space $K\left( X,\,Y \right)$ of compact operators in the space 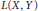$L\left( X,\,Y \right)$ of all bounded linear maps from 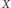$X$ to $Y$.

Keywords

46B2846B1546B20spaces of operatorscomplemented subspaceweakly compact operatorbasic sequence
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 1 , 01 March 2010 , pp. 118 - 121
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Bator, E. and Lewis, P., Complemented spaces of operators. Bull. Polish Acad. Sci. Math. 50(2002), no. 4, 413–416.Google Scholar
[2] Diestel, J., Sequences and Series in Banach Spaces. Graduate Texts in Mathematics 92, Springer-Verlag, New York, 1984.Google Scholar
[3] Diestel, J. and Uhl, J. J. Jr., Vector Measures. Mathematical Surveys 15, American Mathematical Society, Providence, RI, 1977.Google Scholar
[4] Emmanuele, G., Remarks on the uncomplemented subspace W(E, F) . J. Funct. Anal. 99(1991), no. 1, 125–130. doi:10.1016/0022-1236(91)90055-AGoogle Scholar
[5] Emmanuele, G., A remark on the containment of c 0 in spaces of compact operators. Math. Proc. Cambridge Phil. Soc. 111(1992), no. 2, 331–335. doi:10.1017/S0305004100075435Google Scholar
[6] Emmanuele, G. and John, K., Uncomplementability of spaces of compact operators in larger spaces of operators. Czechoslovak Math. J. 47(1997), no. 1, 19–31. doi:10.1023/A:1022483919972Google Scholar
[7] Feder, M., On the non-existence of a projection onto the space of compact operators. Canad. Math. Bull. 25(1982), no. 1, 78–81.Google Scholar
[8] John, K., On the uncomplemented subspace K(X, Y) . Czechoslovak Math. J. 42(1992), no. 1, 167–173.Google Scholar
[9] Kalton, N., Spaces of compact operators. Math. Ann. 208(1974), 267–278. doi:10.1007/BF01432152Google Scholar