Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T00:44:06.578Z Has data issue: false hasContentIssue false
  • English
  • Français

Twisted Conjugacy Classes in Abelian Extensions of Certain Linear Groups

Published online by Cambridge University Press:  20 November 2018

T. Mubeena  and
P. Sankaran
T. Mubeena
Affiliation:
The Institute of Mathematical Sciences, CIT Campus, Taramani, Chennai 600113, India e-mail: [email protected]@imsc.res.in
P. Sankaran
Affiliation:
The Institute of Mathematical Sciences, CIT Campus, Taramani, Chennai 600113, India e-mail: [email protected]@imsc.res.in
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

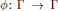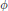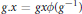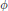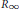Given a group automorphism $\phi :\,\Gamma \,\to \,\Gamma $, one has an action of $\Gamma $ on itself by $\phi $-twisted conjugacy, namely, $g.x\,=\,gx\phi ({{g}^{-1}})$. The orbits of this action are called $\phi $-twisted conjugacy classes. One says that $\Gamma $ has the ${{R}_{\infty }}$-property if there are infinitely many 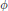$\phi $-twisted conjugacy classes for every automorphism 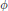$\phi $ of $\Gamma $. In this paper we show that 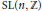$\text{SL(}n\text{,}\mathbb{Z}\text{)}$ and its congruence subgroups have the 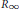${{R}_{\infty }}$-property. 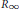Further we show that any (countable) abelian extension of $\Gamma $ has the ${{R}_{\infty }}$-property where $\Gamma $ is a torsion free non-elementary hyperbolic group, or 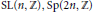$\text{SL(}n\text{,}\mathbb{Z}\text{)},\text{Sp(2}n\text{,}\mathbb{Z}\text{)}$ or a principal congruence subgroup of 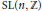$\text{SL(}n\text{,}\mathbb{Z}\text{)}$ or the fundamental group of a complete Riemannian manifold of constant negative curvature.

Keywords

20E45twisted conjugacy classeshyperbolic groupslattices in Lie groups
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 1 , 14 March 2014 , pp. 132 - 140
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Brauer, R., Representations of finite groups. In: 1963 Lectures on Modern Mathematics, Vol. I, Wiley, New York, 1963, pp. 133–175.Google Scholar
[2] Bridson, M. R. and Haefliger, A. Metric spaces of non-positive curvature. Grundlehren der MathematischenWissenschaften, 319, Springer-Verlag, Berlin, 1999.Google Scholar
[3] Fel'shtyn, A. L., The Reidemeister number of any automorphism of a Gromov hyperbolic group isinfinite. Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 279 (2001), Geom. i Topol., 6, 229–240, 250; translation in Math. Sci. (N.Y.) 119 (2004), no. 1, 117–123.Google Scholar
[4] Fel'shtyn, A. L., New directions in Nielsen–Reidemeister theory. Topology Appl. 157 (2010), no. 10–11, 1724–1735. http://dx.doi.org/10.1016/j.topol.2010.02.018 Google Scholar
[5] Fel’shtyn, A. and Gonçalves, D. L., Twisted conjugacy classes in symplectic groups, mapping classgroups and braid groups. With an appendix written jointly with Francois Dahmani. Geom. Dedicata 146 (2010), 211–223. http://dx.doi.org/10.1007/s10711-009-9434-6 Google Scholar
[6] Fel’shtyn, A. and Hill, R., The Reidemeister zeta function with applications to Nielsen theory and aconnection with Reidemeister torsion. K-Theory 8 (1994), no. 4, 367–393. http://dx.doi.org/10.1007/BF00961408 Google Scholar
[7] Gonçalves, D. L. and Wong, P., Twisted conjugacy classes in nilpotent groups. J. Reine Angew. Math. 633 (2009), 11–27. http://dx.doi.org/10.1515/CRELLE.2009.058 Google Scholar
[8] Hua, L. K. and Reiner, I., Automorphisms of the unimodular group. Trans. Amer. Math. Soc. 71 (1951), 331–348. http://dx.doi.org/10.1090/S0002-9947-1951-0043847-X Google Scholar
[9] Levitt, G. and Lustig, M., Most automorphisms of a hyperbolic group have very simple dynamics. Ann. Sci. Ecol. Norm. Sup. 33 (2000) 507–517.Google Scholar
[10] Lyndon, R. and Schupp, P., Combinatorial group theory. Reprint of the 1977 edition, Classics in Mathematics, Springer-Verlag, Berlin, 2001.Google Scholar
[11] Nasybullov, T. R., Twisted conjugacy classes in special and general linear groups. arxiv:1201.6515. Google Scholar
[12] Newman, M., Normalizers of modular groups. Math. Ann. 238 (1978), no. 2, 123–129. http://dx.doi.org/10.1007/BF01424769 Google Scholar
[13] O'Meara, O. T., The automorphisms of the linear groups over any integral domain. J. Rein. Angew. Math. 223 (1966), 56–100.Google Scholar
[14] Osin, D., Small cancellations over relatively hyperbolic groups and embedding theorems. Ann. of Math. (2) 172 (2010), no. 1, 1–39. http://dx.doi.org/10.4007/annals.2010.172.1 Google Scholar
[15] Pyber, L., Finite groups have many conjugacy classes. J. London Math. Soc. 46 (1992), no. 2, 239–249. http://dx.doi.org/10.1112/jlms/s2-46.2.239 Google Scholar
[16] Raghunathan, M. S., Discrete subgroups of Lie groups. Ergebnisse der Mathematik und ihrer Grenzgebiete, 68, Springer-Verlag, New York-Heidelberg, 1972.Google Scholar
[17] Reiner, I., Automorphisms of the symplectic modular group. Trans. Amer. Math. Soc. 80 (1955), 35–50. http://dx.doi.org/10.1090/S0002-9947-1955-0073603-1 Google Scholar
[18] Sela, Z., Endomorphisms of hyperbolic groups. I. The Hopf property. Topology 38 (1999), no. 2, 301–321. http://dx.doi.org/10.1016/S0040-9383(98)00015 Google Scholar
[19] Serre, J.-P., Trees. Translated from the French original by John Stillwell. Corrected 2nd printing of the 1980 English translation, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
[20] Sury, B., Congruence subgroup property. An elementary approach aimed at applications. Texts and Readings in Mathematics, 24, Hindustan Book Agency, New Delhi, 2003.Google Scholar
[21] Zimmer, R. J., Ergodic theory and semisimple Lie groups. Monographs in Mathematics, 81, Birkhäuser Verlag, Basel, 1984.Google Scholar