Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-29T04:49:24.779Z Has data issue: false hasContentIssue false
  • English
  • Français

Trivial Units in Group Rings

Published online by Cambridge University Press:  20 November 2018

Daniel R. Farkas  and
Peter A. Linnell
Daniel R. Farkas
Affiliation:
Department of Mathematics Virginia Polytechnic Institute and State University Blacksburg, Virginia 24061-0123 U.S.A., website: http://www.math.vt.edu/people/farkas/ email: [email protected]
Peter A. Linnell
Affiliation:
Department of Mathematics Virginia Polytechnic Institute and State University Blacksburg, Virginia 24061-0123 U.S.A., website: http://www.math.vt.edu/people/linnell/ email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 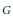$G$ be an arbitrary group and let $U$ be a subgroup of the normalized units in 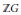$\mathbb{Z}G$. We show that if $U$ contains 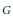$G$ as a subgroup of finite index, then 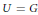$U\,=\,G$. This result can be used to give an alternative proof of a recent result of Marciniak and Sehgal on units in the integral group ring of a crystallographic group.

Keywords

16S3416U60unitstracefinite conjugate subgroup
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 1 , 01 March 2000 , pp. 60 - 62
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Marciniak, Z. S. and Sehgal, S. K., Units in group rings and geometry.Methods in Ring Theory, Levico Terme, Italy, (eds., V. S. Drensky, A. Giambruno, and S. K. Sehgal), Lecture Notes in Pure and Applied Math. 198, Marcel Dekker, New York, 1998, 185–198.Google Scholar
[2] Sehgal, S. K., Topics in group rings. Pure and Applied Math. 50, Marcel Dekker, New York, 1978.Google Scholar
[3] Sehgal, S. K., Units in integral group rings. Pitman Monographs and Surveys in Pure and Applied Math. 69, Longman Scientific, Harlow, 1993.Google Scholar