Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Goodman-Strauss, Chaim
2001.
Compass and Straightedge in the Poincaré Disk.
The American Mathematical Monthly,
Vol. 108,
Issue. 1,
p.
38.
Baek, S. K
Minnhagen, P
and
Kim, B. J
2007.
Phase transition of XY model in heptagonal lattice.
Europhysics Letters (EPL),
Vol. 79,
Issue. 2,
p.
26002.
Baek, Seung Ki
Yi, Su Do
and
Kim, Beom Jun
2008.
Diffusion on a heptagonal lattice.
Physical Review E,
Vol. 77,
Issue. 2,
Hall, Rachel Wells
2008.
The mathematical art exhibition at BRIDGES: mathematical connections in art, music and science, Leeuwarden, the Netherlands, July 2008.
Journal of Mathematics and the Arts,
Vol. 2,
Issue. 4,
p.
197.
Baek, Seung Ki
Minnhagen, Petter
Shima, Hiroyuki
and
Kim, Beom Jun
2009.
Phase transition ofq-state clock models on heptagonal lattices.
Physical Review E,
Vol. 80,
Issue. 1,
Baek, Seung Ki
Shima, Hiroyuki
and
Kim, Beom Jun
2009.
Curvature-induced frustration in theXYmodel on hyperbolic surfaces.
Physical Review E,
Vol. 79,
Issue. 6,
Baek, Seung Ki
Minnhagen, Petter
and
Kim, Beom Jun
2009.
Percolation on hyperbolic lattices.
Physical Review E,
Vol. 79,
Issue. 1,
Basteiro, Pablo
Di Giulio, Giuseppe
Erdmenger, Johanna
Karl, Jonathan
Meyer, Rene
and
Xian, Zhuo-Yu
2022.
Towards explicit discrete holography: Aperiodic spin chains from hyperbolic tilings.
SciPost Physics,
Vol. 13,
Issue. 5,
Basteiro, Pablo
Dusel, Felix
Erdmenger, Johanna
Herdt, Dietmar
Hinrichsen, Haye
Meyer, René
and
Schrauth, Manuel
2023.
Breitenlohner-Freedman Bound on Hyperbolic Tilings.
Physical Review Letters,
Vol. 130,
Issue. 9,
Basteiro, Pablo
Nath Das, Rathindra
Di Giulio, Giuseppe
and
Erdmenger, Johanna
2023.
Aperiodic spin chains at the boundary of hyperbolic tilings.
SciPost Physics,
Vol. 15,
Issue. 5,
Schrauth, Manuel
Thurn, Yanick
Goth, Florian
Portela, Jefferson
Herdt, Dietmar
and
Dusel, Felix
2024.
Codebase release 1.3 for HYPERTILING.
SciPost Physics Codebases,
Schrauth, Manuel
Thurn, Yanick
Goth, Florian
Portela, Jefferson
Herdt, Dietmar
and
Dusel, Felix
2024.
HYPERTILING — a high performance Python library for the generation and visualization of hyperbolic lattices.
SciPost Physics Codebases,
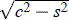 , while its centre is at distance 1/ tanh ψ = c/z from A. In the hyperbolic triangle ABC, the altitude from AB to the right-angled vertex C is ζ, where sinh ζ = z.
, while its centre is at distance 1/ tanh ψ = c/z from A. In the hyperbolic triangle ABC, the altitude from AB to the right-angled vertex C is ζ, where sinh ζ = z.