Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T17:30:18.821Z Has data issue: false hasContentIssue false
  • English
  • Français

Transversals with Residue in Moderately Overlapping T(k)-Families of Translates

Published online by Cambridge University Press:  20 November 2018

Aladár Heppes
Aladár Heppes*
Affiliation:
Rényi Institute of the Hungarian Academy of Sciences, Reáltanoda u. 13-15, H-1053 Budapest, Hungary e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 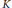$K$ denote an oval, a centrally symmetric compact convex domain with non-empty interior. A family of translates of 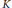$K$ is said to have property 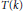$T\left( k \right)$ if for every subset of at most $k$ translates there exists a common line transversal intersecting all of them. The integer $k$ is the stabbing level of the family. 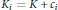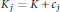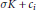Two translates ${{K}_{i}}\,=\,K\,+\,{{c}_{i}}$ and ${{K}_{j}}\,=\,K\,+\,{{c}_{j}}$ are said to be $\sigma$-disjoint if $\sigma K\,+\,{{c}_{i}}$ and 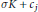$\sigma K\,+\,{{c}_{j}}$ are disjoint. A recent Helly-type result claims that for every 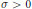$\sigma \,>\,0$ there exists an integer 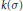$k\left( \sigma \right)$ such that if a family of $\sigma$-disjoint unit diameter discs has property 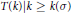$T\left( k \right)|k\ge k\left( \sigma \right)$, then there exists a straight line meeting all members of the family. In the first part of the paper we give the extension of this theorem to translates of an oval $k$. The asymptotic behavior of 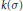$k\left( \sigma \right)$ for 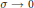$\sigma \,\to \,0$ is considered as well.

Katchalski and Lewis proved the existence of a constant $r$ such that for every pairwise disjoint family of translates of an oval 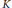$K$ with property 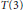$T\left( 3 \right)$ a straight line can be found meeting all but at most $r$ members of the family. In the second part of the paper $\sigma$-disjoint families of translates of 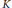$K$ are considered and the relation of $\sigma$ and the residue $r$ is investigated. The asymptotic behavior of 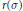$r\left( \sigma \right)$ for 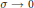$\sigma \,\to \,0$ is also discussed.

Keywords

52A35transversalσ-disjointT(k)-familyHelly numberresidue
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 3 , 01 September 2009 , pp. 388 - 402
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Aronov, B., Goodman, J. E., Pollack, R., and Wenger, R., On the Helly number for hyperplane transversals to unit balls, Discrete Comput. Geom. 24(2000), no. 2-3, 171–176.Google Scholar
[2] Bezdek, A., On the transversal-conjecture of Katchalski and Lewis. In: Intuitive Geometry. Colloquia Math. Soc. János Bolya 63, North-Holland, Amsterdam, 1991, pp. 23–25.Google Scholar
[3] Bezdek, K., Bisztriczky, T., Csikós, B., and Heppes, A., On the transversal Helly numbers of disjoint and overlapping discs. Arch. Math. 87(2006), no. 1, 86–96.Google Scholar
[4] Bisztriczky, T., Fodor, F., and Oliveros, D., Large transversals to small families of unit disks. Acta Math. Hungar. 106(2005), no. 4, 285–291.Google Scholar
[5] Bisztriczky, T., Fodor, F., and Oliveros, D., A transversal property of families of eight or nine unit disks. Bol. Soc. Mat. Mexicana 12(2006), no. 1, 59–73.Google Scholar
[6] Bisztriczky, T., Fodor, F., and Oliveros, D., The T(4) property for families of unit disks. Israel J. Math. 168(2008), 239–252.Google Scholar
[7] Danzer, L., Über ein Problem aus der kombinatorischen Geometrie. Arch. Math. 8(1957), 347–351.Google Scholar
[8] Eckhoff, J., Transversalenprobleme in der Ebene. Arch.Math. 24(1973), 195–202.Google Scholar
[9] Eckhoff, J., Helly, Radon and Carathéodory type theorems. In: Handbook of Convex Geometry. Amsterdam, North-Holland, 1993, pp. 389–448.Google Scholar
[10] Tóth, L. Fejes, Regular Figures. Pergamon Press, New York, 1964.Google Scholar
[11] Goodman, J. E., Pollack, R., and Wenger, R., Geometric transversal theory. In: New trends in Discrete and Computational Geometry, Algorithms Combin. 10. Springer, Berlin, 1993, pp. 163–198.Google Scholar
[12] Grünbaum, B., On common transversals. Arch. Math. 9(1958), 465–469.Google Scholar
[13] Heppes, A., The width of the transversal strips of T(3)-families in the plane. Discrete Comput. Geom. 34(2005), no. 3, 455–461.Google Scholar
[14] Heppes, A., New upper bound on the transversal width of T(3)-families of discs. Discrete Comput. Geom. 34(2005), no. 3, 463–474.Google Scholar
[15] Heppes, A., Proof of the Katchalski-Lewis transversal conjecture for T(3)-families of congruent discs. Discrete Comput. Geom. 38(2007), no. 2, 289–304.Google Scholar
[16] Holmsen, A., New bounds on the Katchalski-Lewis transversal problem. Discrete Comput. Geom. 29(2003), 395–408.Google Scholar
[17] Holmsen, A., Recent progress on line transversals to families of translated ovals. In: Surveys on Discrete and Computational Geometry, Contemp. Math. 453. American Mathematical Society, Providence, RI, 2008, pp 283–297.Google Scholar
[18] Kaiser, T., Line transversals to unit discs. Discrete Comput. Geom. 28(2002), no. 3, 379–387.Google Scholar
[19] Katchalski, M., A conjecture of Grünbaum on common transversals. Math. Scand. 59(1986), no. 2, 192–198.Google Scholar
[20] Katchalski, M. and Lewis, T., Cutting families of convex sets. Proc. Amer. Math. Soc. 79(1980), no. 3, 457–461.Google Scholar
[21] Lay, S., Convex Sets and Their Applications. John Wiley & Sons, New York, 1982.Google Scholar
[22] Tverberg, H., Proof of Grünbaum's conjecture on common transversals for translates. Discrete Comput. Geom. 4(1989), no. 3, 191–203.Google Scholar
[23] Wenger, R., Helly-type theorems and geometric transversals. In: Handbook of Discrete and Computational Geometry. Second edition, CRC Press, Boca Raton, FL, 2004, pp. 63–82.Google Scholar