Article contents
Trace Classes and Quadratic Forms in the Modular Group
Published online by Cambridge University Press: 20 November 2018
Abstract
The Modular Group M is PSL2(Z) the group of linear fractional transformations with integral entries and determinant one. M has been of great interest in many diverse fields of Mathematics, including Number Theory, Automorphic Function Theory and Group Theory. In this paper we give an effective algorithm to determine, for each integer d, a complete set of representatives for the trace classes in trace d. This algorithm depends on the combinatorial group theoretic structure of M. It has been subsequently extended by Sheingorn to the general Hecke groups. The number h(d) of trace classes in trace d is equal to the ideal class number of the field 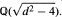 The algorithm mentioned above then provides a new straightforward computational procedure for determining h(d). Finally as an outgrowth of the algorithm we present a wide generalization of the Fermat Two-Square theorem. This last result can also be derived from classical work of Gauss.
The algorithm mentioned above then provides a new straightforward computational procedure for determining h(d). Finally as an outgrowth of the algorithm we present a wide generalization of the Fermat Two-Square theorem. This last result can also be derived from classical work of Gauss.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1994
References
- 7
- Cited by


