Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T03:18:56.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Total Nonnegativity and Stable Polynomials

Published online by Cambridge University Press:  20 November 2018

Kevin Purbhoo
Kevin Purbhoo*
Affiliation:
Department of Combinatorics and Optimization, University of Waterloo, 200 University Ave. W., Waterloo, ON N2L 3G1, e-mail : [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider homogeneous multiaffine polynomials whose coefficients are the Plücker coordinates of a point 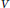$V$ of the Grassmannian. We show that such a polynomial is stable (with respect to the upper half plane) if and only if 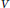$V$ is in the totally nonnegative part of the Grassmannian. To prove this, we consider an action of matrices on multiaffine polynomials. We show that a matrix $A$ preserves stability of polynomials if and only if $A$ is totally nonnegative. The proofs are applications of classical theory of totally nonnegative matrices, and the generalized Pólya-Schur theory of Borcea and Brändén.

Keywords

32A6014M1514P1015B48stable polynomialzeros of a complex polynomialtotal nonnegative Grassmanniantotally nonnegative matrix
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 4 , 01 December 2018 , pp. 836 - 847
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Borcea, J. and Brândén, P., The Lee-Yang and Pôlya-Schur programs I: linear operators preserving stability. Invent. Math. 177 (2009), 541–569. http://dx.doi.Org/10.1007/s00222-009-0189-3Google Scholar
[2] Borcea, J. and Brândén, P., The Lee-Yang and Pôlya-Schur programs II: theory of stable polynomials and applications. Comm. Pure Appl. Math. 62 (2009), 1595–1631. http://dx.doi.org/!0.1002/cpa.20295Google Scholar
[3] Borcea, J., Brândén, P., and Liggett, T. M., Negative dependence and the geometry of polynomials. J. Amer. Math. Soc. 22 (2009), 521–567. http://dx.doi.org/10.1090/S0894-0347-08-00618-8Google Scholar
[4] Brândén, P., Polynomials with the half-plane property and matroid theory. Adv. Math. 216 (2007), 302–320. http://dx.doi.Org/10.1016/j.aim.2007.05.011Google Scholar
[5] Choe, Y.-B., Oxley, J. G., Sokal, A. D., and Wagner, D. G., Homogeneous multivariate polynomials with the half-plane property. Adv. in Appl. Math. 32 (2004), 88–187. http://dx.doi.Org/10.1016/S0196-8858(03)00078-2Google Scholar
[6] Fomin, S., Total positivity and cluster algebras. Proceedings of the International Congress of Mathematicians, Vol. II, Hindustan Book Agency, New Delhi, 2010, pp. 125–145.Google Scholar
[7] Grace, J. H., The zeros of a polynomial, Proc. Cambridge Philos. Soc. 11 (1902), 352–357.Google Scholar
[8] Knutson, A., Schubert calculus and shifting of interval positroid varieties. arxiv:1408.12 61Google Scholar
[9] Knutson, A., Lam, T., and Speyer, D., Positroid varieties: juggling and geometry. Compos. Math. 198 (2013), 1710–1752. http://dx.doi.Org/10.1112/S0010437X13007240Google Scholar
[10] Kodama, Y. and Williams, L. K., KP solitons and total positivity for the Grassmannian. Invent. Math. 198 (2014), 637–699. http://dx.doi.org/10.1007/s00222-014-0506-3Google Scholar
[11] Loewner, C., On totally positive matrices. Math. Z. 63(1955) 338-340. http://dx.doi.Org/10.1007/BF01187945Google Scholar
[12] Lusztig, G., Total positivity in partial flag manifolds. Represent. Theory 2 (1998), 70–78. http://dx.doi.Org/10.1090/S1088-4165-98-00046-6Google Scholar
[13] Marcott, C., Positroids have the Rayleigh property. arxiv:1611.03583Google Scholar
[14] Marsh, R. J. and Rietsch, K., Parametrizations in flag varieties. Represent. Theory 8 (2004), 212–242. http://dx.doi.Org/1 0.1090/S1088-41 65-04-00230-4Google Scholar
[15] Postnikov, A., Total positivity, Grassmannians, and networks. arxiv:0609764Google Scholar
[16] Rietsch, K., Total positivity and real flag varieties. Ph.D. Dissertation, MIT, 1998.Google Scholar
[17] Szegô, G., Bemerkungen zu einem Satz von f.H. Grace tiber die Wurzeln algebraischer Gleichungen. Math. Z. 13 (1922), 28–55. http://dx.doi.org/10.1007/BF01485280Google Scholar
[18] Wagner, D. G., Multivariate stable polynomials: theory and applications. Bull. Amer. Math. Soc. 48 (2011), 53–84. http://dx.doi.org/10.1090/S0273-0979-2010-01321-5Google Scholar
[19] Walsh, J. L., On the location of the roots of certain types of polynomials. Trans. Amer. Math. Soc. 24 (1922), 163–180. http://dx.doi.org/10.1090/S0002-9947-1922-1501220-0Google Scholar
[20] Whitney, A. M., A reduction theorem for totally positive matrices. J. Analyse Math. 2 (1952), 88–92. http://dx.doi.org/10.1007/BF02786969Google Scholar
[21] Williams, L. K., Enumeration of totally positive Grassmann cells. Adv. Math 190 (2005), 319–342. http://dx.doi.Org/10.1016/j.aim.2004.01.003Google Scholar