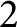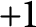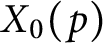1 Introduction
The study of diagonal cycles on triple products of Shimura curves has its origins in the work of Gross, Kudla, and Schoen [Reference Gross and Kudla11, Reference Gross and Schoen12]. They introduced a null-homologous modification of the diagonal embedding of the curve in its triple product, referred to as the modified diagonal cycle, or more commonly today as the Gross–Kudla–Schoen cycle. Given three cuspidal newforms of weight
![]() $2$
and square-free level N such that the sign of the functional equation of the associated triple product L-function is
$2$
and square-free level N such that the sign of the functional equation of the associated triple product L-function is
![]() $-1$
, Gross and Kudla [Reference Gross and Kudla11] conjectured that the central value at
$-1$
, Gross and Kudla [Reference Gross and Kudla11] conjectured that the central value at
![]() $s=2$
of the derivative of this L-function is given by a complex period times the Beilinson–Bloch height of the corresponding Hecke isotypic component of the modified diagonal cycle on the triple product of an indefinite Shimura curve determined by the local triple product root numbers. A proof of this conjecture was announced in work of Yuan et al. [Reference Yuan, Zhang and Zhang28], but has yet to be published. The Shimura curve in question is the modular curve
$s=2$
of the derivative of this L-function is given by a complex period times the Beilinson–Bloch height of the corresponding Hecke isotypic component of the modified diagonal cycle on the triple product of an indefinite Shimura curve determined by the local triple product root numbers. A proof of this conjecture was announced in work of Yuan et al. [Reference Yuan, Zhang and Zhang28], but has yet to be published. The Shimura curve in question is the modular curve
![]() $X_0(N)$
precisely when the local triple product root numbers are
$X_0(N)$
precisely when the local triple product root numbers are
![]() $+1$
at all finite places.
$+1$
at all finite places.
1.1 Main results
In this article, we exhibit certain torsion properties of modified diagonal classesFootnote
1
on the triple product of the modular curve
![]() $X:=X_0(p)$
defined over
$X:=X_0(p)$
defined over
![]() $\mathbb {Q}$
and of prime level p. The results hold more generally for composite square-free level N (see Section 1.4). Since the prime level case already contains all relevant ingredients of the proof, we have chosen to focus on this case.
$\mathbb {Q}$
and of prime level p. The results hold more generally for composite square-free level N (see Section 1.4). Since the prime level case already contains all relevant ingredients of the proof, we have chosen to focus on this case.
The modified diagonal cycle depends on a base point e in
![]() $X(\bar {\mathbb {Q}})$
. It will be denoted by
$X(\bar {\mathbb {Q}})$
. It will be denoted by
![]() $\Delta _{\operatorname {\mathrm {GKS}}}(e)$
and viewed as an element of the Chow group
$\Delta _{\operatorname {\mathrm {GKS}}}(e)$
and viewed as an element of the Chow group
![]() $\operatorname {\mathrm {CH}}^2(X^3)_0(\bar {\mathbb {Q}})$
of null-homologous codimension
$\operatorname {\mathrm {CH}}^2(X^3)_0(\bar {\mathbb {Q}})$
of null-homologous codimension
![]() $2$
algebraic cycles on
$2$
algebraic cycles on
![]() $X^3$
over
$X^3$
over
![]() $\bar {\mathbb {Q}}$
modulo rational equivalence (see Section 1.7 for our slightly unconventional definition of Chow groups as functors). Let
$\bar {\mathbb {Q}}$
modulo rational equivalence (see Section 1.7 for our slightly unconventional definition of Chow groups as functors). Let
![]() $f_1, f_2$
, and
$f_1, f_2$
, and
![]() $f_3$
be three normalized cuspidal eigenforms of weight
$f_3$
be three normalized cuspidal eigenforms of weight
![]() $2$
and level
$2$
and level
![]() $\Gamma _0(p)$
, and denote by
$\Gamma _0(p)$
, and denote by
![]() $F:=f_1\otimes f_2\otimes f_3$
their triple product. We place ourselves in the setting where the global root number
$F:=f_1\otimes f_2\otimes f_3$
their triple product. We place ourselves in the setting where the global root number
![]() $W(F)$
of the triple product L-function
$W(F)$
of the triple product L-function
![]() $L(F,s)$
associated with F is
$L(F,s)$
associated with F is
![]() $+1$
. This assumption forces
$+1$
. This assumption forces
![]() $L(F, s)$
to vanish to even order at its centre
$L(F, s)$
to vanish to even order at its centre
![]() $s=2$
. Comparing with the more classical situation of Heegner points studied in the seminal work of Gross and Zagier [Reference Gross and Zagier13], it seems reasonable to expect that the “F-isotypic Hecke component”
$s=2$
. Comparing with the more classical situation of Heegner points studied in the seminal work of Gross and Zagier [Reference Gross and Zagier13], it seems reasonable to expect that the “F-isotypic Hecke component”
![]() $\Delta _{\operatorname {\mathrm {GKS}}}^F(e)$
(see Remark 3.2) of the modified diagonal cycle, with
$\Delta _{\operatorname {\mathrm {GKS}}}^F(e)$
(see Remark 3.2) of the modified diagonal cycle, with
![]() $e\in X(\mathbb {Q})$
, is trivial in the Chow group
$e\in X(\mathbb {Q})$
, is trivial in the Chow group
![]() $\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})\otimes _{\mathbb {Z}} K_F$
of cycles defined over
$\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})\otimes _{\mathbb {Z}} K_F$
of cycles defined over
![]() $\mathbb {Q}$
with coefficients in the Hecke field of F, in line with the predictions of the Beilinson–Bloch conjectures [Reference Bloch4]. While it appears difficult to prove a torsion statement directly in the Chow group, we can prove the corresponding result for the image of
$\mathbb {Q}$
with coefficients in the Hecke field of F, in line with the predictions of the Beilinson–Bloch conjectures [Reference Bloch4]. While it appears difficult to prove a torsion statement directly in the Chow group, we can prove the corresponding result for the image of
![]() $\Delta _{\operatorname {\mathrm {GKS}}}^F(e)$
under the complex Abel–Jacobi map
$\Delta _{\operatorname {\mathrm {GKS}}}^F(e)$
under the complex Abel–Jacobi map
whose target is the Griffiths intermediate Jacobian of
![]() $X^3_{\mathbb {C}}$
viewed as a complex manifold.
$X^3_{\mathbb {C}}$
viewed as a complex manifold.
Theorem 1.1 Let
![]() $f_1, f_2$
, and
$f_1, f_2$
, and
![]() $f_3$
be three normalized eigenforms of weight
$f_3$
be three normalized eigenforms of weight
![]() $2$
and level
$2$
and level
![]() $\Gamma _0(p)$
, denote by
$\Gamma _0(p)$
, denote by
![]() $F=f_1\otimes f_2\otimes f_3$
their triple product, and suppose that the global root number of
$F=f_1\otimes f_2\otimes f_3$
their triple product, and suppose that the global root number of
![]() $L(F, s)$
is
$L(F, s)$
is
![]() $+1$
. Then
$+1$
. Then
![]() $\operatorname {\mathrm {AJ}}_{X^3}(\Delta _{\operatorname {\mathrm {GKS}}}^F(e))$
is trivial in
$\operatorname {\mathrm {AJ}}_{X^3}(\Delta _{\operatorname {\mathrm {GKS}}}^F(e))$
is trivial in
![]() $J^2(X^3_{\mathbb {C}})\otimes _{\mathbb {Z}} K_F$
, for all
$J^2(X^3_{\mathbb {C}})\otimes _{\mathbb {Z}} K_F$
, for all
![]() $e \text{ in } X(\mathbb {Q})$
.
$e \text{ in } X(\mathbb {Q})$
.
The kernel of the complex Abel–Jacobi map (restricted to cycles defined over
![]() $\bar {\mathbb {Q}}$
) is conjectured to be torsion [Reference Jannsen16, Conjecture 9.12]. Conditional on this conjecture, Theorem 1.1 implies that
$\bar {\mathbb {Q}}$
) is conjectured to be torsion [Reference Jannsen16, Conjecture 9.12]. Conditional on this conjecture, Theorem 1.1 implies that
![]() $\Delta _{\operatorname {\mathrm {GKS}}}^F(e)$
is trivial in
$\Delta _{\operatorname {\mathrm {GKS}}}^F(e)$
is trivial in
![]() $\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})\otimes _{\mathbb {Z}} K_F$
. The same statement as in Theorem 1.1 holds with the complex Abel–Jacobi map replaced by its
$\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})\otimes _{\mathbb {Z}} K_F$
. The same statement as in Theorem 1.1 holds with the complex Abel–Jacobi map replaced by its
![]() $\ell $
-adic étale counterpart [Reference Bloch4]
$\ell $
-adic étale counterpart [Reference Bloch4]
 $$\begin{align*}\operatorname{\mathrm{AJ}}^{\operatorname{\mathrm{et}}}_{X^3} : \operatorname{\mathrm{CH}}^2(X^3)_0(\mathbb{Q}) {\longrightarrow} H^1(\mathbb{Q}, H^{3}_{\operatorname{\mathrm{et}}}(X^3_{\bar{\mathbb{Q}}}, \mathbb{Q}_\ell(2))), \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{AJ}}^{\operatorname{\mathrm{et}}}_{X^3} : \operatorname{\mathrm{CH}}^2(X^3)_0(\mathbb{Q}) {\longrightarrow} H^1(\mathbb{Q}, H^{3}_{\operatorname{\mathrm{et}}}(X^3_{\bar{\mathbb{Q}}}, \mathbb{Q}_\ell(2))), \end{align*}$$
with
![]() $\ell $
a rational prime (see Remark 4.4).
$\ell $
a rational prime (see Remark 4.4).
In the special case
![]() $p=37$
, using numerical results due to Stein [Reference Darmon, Daub, Lichtenstein and Rotger5, Appendix], we deduce the following, where
$p=37$
, using numerical results due to Stein [Reference Darmon, Daub, Lichtenstein and Rotger5, Appendix], we deduce the following, where
![]() $\xi _\infty $
denotes the cusp of X at infinity.
$\xi _\infty $
denotes the cusp of X at infinity.
Theorem 1.2 Let f and g be the normalized eigenforms of weight
![]() $2$
and level
$2$
and level
![]() $\Gamma _0(37)$
corresponding to the elliptic curves with Cremona labels
$\Gamma _0(37)$
corresponding to the elliptic curves with Cremona labels
![]() $37$
b and
$37$
b and
![]() $37$
a, and let
$37$
a, and let
![]() $F:=g\otimes g\otimes f$
. Then
$F:=g\otimes g\otimes f$
. Then
 $\operatorname {\mathrm {AJ}}_{X_0(37)^3}(8\Delta _{\operatorname {\mathrm {GKS}}}^F(\xi _\infty ))$
is a nontrivial
$\operatorname {\mathrm {AJ}}_{X_0(37)^3}(8\Delta _{\operatorname {\mathrm {GKS}}}^F(\xi _\infty ))$
is a nontrivial
![]() $6$
-torsion element of
$6$
-torsion element of
![]() $J^2(X_0(37)^3_{\mathbb {C}})$
.
$J^2(X_0(37)^3_{\mathbb {C}})$
.
1.2 Application to Chow–Heegner points
Chow–Heegner points were introduced by Bertolini et al. [Reference Bertolini, Darmon and Prasanna2] as a generalization of the construction of Heegner points. The idea is to produce rational points on elliptic curves by pushing forward algebraic cycles on higher dimensional varieties using suitable correspondences, or generalized modular parametrizations, as they are referred to in [Reference Bertolini, Darmon and Prasanna2].
Let f be a normalized cuspidal eigenform of weight
![]() $2$
and level
$2$
and level
![]() $\Gamma _0(p)$
with rational Fourier coefficients. Denote by
$\Gamma _0(p)$
with rational Fourier coefficients. Denote by
![]() $E_f$
the optimal elliptic curve over
$E_f$
the optimal elliptic curve over
![]() $\mathbb {Q}$
of conductor p associated with f by Eichler and Shimura [Reference Shimura27]. Using an auxiliary normalized cuspidal eigenform g of weight
$\mathbb {Q}$
of conductor p associated with f by Eichler and Shimura [Reference Shimura27]. Using an auxiliary normalized cuspidal eigenform g of weight
![]() $2$
and level
$2$
and level
![]() $\Gamma _0(p)$
, it is possible to construct a correspondence
$\Gamma _0(p)$
, it is possible to construct a correspondence
 $\Pi _{g}^f \in \operatorname {\mathrm {CH}}^2(X^3\times E_f)(\mathbb {Q})$
, which gives rise via push-forward to a generalized modular parametrization, that is, a natural transformation
$\Pi _{g}^f \in \operatorname {\mathrm {CH}}^2(X^3\times E_f)(\mathbb {Q})$
, which gives rise via push-forward to a generalized modular parametrization, that is, a natural transformation
 $$\begin{align*}\Pi_{g,*}^f : \operatorname{\mathrm{CH}}^2(X^3)_0 {\longrightarrow} \operatorname{\mathrm{CH}}^1(E_f)_0=E_f. \end{align*}$$
$$\begin{align*}\Pi_{g,*}^f : \operatorname{\mathrm{CH}}^2(X^3)_0 {\longrightarrow} \operatorname{\mathrm{CH}}^1(E_f)_0=E_f. \end{align*}$$
The Chow–Heegner point associated with the modified diagonal cycle based at a point
![]() $e\in X(\bar {\mathbb {Q}})$
is then defined as
$e\in X(\bar {\mathbb {Q}})$
is then defined as
 $$ \begin{align*} P_{g}^f(e):=\Pi_{g,*}^f(\Delta_{\operatorname{\mathrm{GKS}}}(e))\in E_f(\bar{\mathbb{Q}}). \end{align*} $$
$$ \begin{align*} P_{g}^f(e):=\Pi_{g,*}^f(\Delta_{\operatorname{\mathrm{GKS}}}(e))\in E_f(\bar{\mathbb{Q}}). \end{align*} $$
Darmon et al. [Reference Darmon, Rotger and Sols7] have studied such points, in the broader context of Shimura curves over totally real fields, notably by computing their images under the complex Abel–Jacobi map in terms of iterated integrals. Methods have been developed by Darmon et al. [Reference Darmon, Daub, Lichtenstein and Rotger5] to numerically calculate such points in the case of modular curves.
Let
![]() $F:=g\otimes g\otimes f$
. We exhibit a correspondence mapping
$F:=g\otimes g\otimes f$
. We exhibit a correspondence mapping
![]() $\Delta _{\operatorname {\mathrm {GKS}}}^F(e)$
to
$\Delta _{\operatorname {\mathrm {GKS}}}^F(e)$
to
 $P_{g}^f(e)$
. When the global root number
$P_{g}^f(e)$
. When the global root number
![]() $W(F)$
is
$W(F)$
is
![]() $-1$
, Darmon et al. [Reference Darmon, Rotger and Sols7] have studied the nontorsion properties of
$-1$
, Darmon et al. [Reference Darmon, Rotger and Sols7] have studied the nontorsion properties of
 $P_{g}^f(\xi _\infty )$
, building on [Reference Yuan, Zhang and Zhang28]. In the complementary situation when
$P_{g}^f(\xi _\infty )$
, building on [Reference Yuan, Zhang and Zhang28]. In the complementary situation when
![]() $W(F)=+1$
, we use Theorem 1.1 and functoriality of Abel–Jacobi maps with respect to correspondences to deduce the following:
$W(F)=+1$
, we use Theorem 1.1 and functoriality of Abel–Jacobi maps with respect to correspondences to deduce the following:
Theorem 1.3 Let f and g be as above, and let
![]() $F=g\otimes g\otimes f$
. If
$F=g\otimes g\otimes f$
. If
![]() $W(F)=+1$
, then the Chow–Heegner point
$W(F)=+1$
, then the Chow–Heegner point
 $P_{g}^f(e)$
is torsion in
$P_{g}^f(e)$
is torsion in
![]() $E_f(\mathbb {Q})$
, for all
$E_f(\mathbb {Q})$
, for all
![]() $e\in X(\mathbb {Q})$
.
$e\in X(\mathbb {Q})$
.
Theorem 1.3 with
![]() $e=\xi _\infty $
recovers a result of Daub [Reference Daub8, Theorem 3.3.8] by a different method in the case of prime level. Similar arguments should work for f not rational.
$e=\xi _\infty $
recovers a result of Daub [Reference Daub8, Theorem 3.3.8] by a different method in the case of prime level. Similar arguments should work for f not rational.
1.3 Strategy of the proof
The key ingredient in the proof of Theorem 1.1 is the Atkin–Lehner involution
![]() $w_p$
of X. The global root number of
$w_p$
of X. The global root number of
![]() $W(F)$
is the product of the global root numbers of
$W(F)$
is the product of the global root numbers of
![]() $f_1, f_2$
, and
$f_1, f_2$
, and
![]() $f_3$
, which are each equal to the negative of their
$f_3$
, which are each equal to the negative of their
![]() $w_p$
-eigenvalue. As a consequence, the assumption that
$w_p$
-eigenvalue. As a consequence, the assumption that
![]() $W(F)$
equals
$W(F)$
equals
![]() $+1$
translates into information about the action of
$+1$
translates into information about the action of
![]() $w_p\times w_p\times w_p$
on F, and consequently on
$w_p\times w_p\times w_p$
on F, and consequently on
![]() $\operatorname {\mathrm {AJ}}_{X^3}(\Delta _{\operatorname {\mathrm {GKS}}}^F(e))$
, as the latter lies in the F-isotypic Hecke component of the intermediate Jacobian by functoriality of the Abel–Jacobi map with respect to correspondences. The work of Mazur [Reference Mazur22] provides necessary information about the rational points
$\operatorname {\mathrm {AJ}}_{X^3}(\Delta _{\operatorname {\mathrm {GKS}}}^F(e))$
, as the latter lies in the F-isotypic Hecke component of the intermediate Jacobian by functoriality of the Abel–Jacobi map with respect to correspondences. The work of Mazur [Reference Mazur22] provides necessary information about the rational points
![]() $X(\mathbb {Q})$
and the action of
$X(\mathbb {Q})$
and the action of
![]() $w_p$
on them.
$w_p$
on them.
1.4 Composite square-free level
The arguments of this paper carry over to the more general setting where the level N is composite, but square-free. This is the situation initially considered in the work of Gross and Kudla [Reference Gross and Kudla11]. It becomes necessary to replace eigenforms by newforms.
Let
![]() $f_1, f_2, f_3$
be three normalized newforms of weight
$f_1, f_2, f_3$
be three normalized newforms of weight
![]() $2$
and level
$2$
and level
![]() $\Gamma _0(N)$
, and let
$\Gamma _0(N)$
, and let
![]() $F:=f_1\otimes f_2\otimes f_3$
. The level being square-free guarantees that the local root numbers
$F:=f_1\otimes f_2\otimes f_3$
. The level being square-free guarantees that the local root numbers
![]() $W_p(F)$
for
$W_p(F)$
for
![]() $p\mid N$
are the products of the local root numbers at p of
$p\mid N$
are the products of the local root numbers at p of
![]() $f_1, f_2$
, and
$f_1, f_2$
, and
![]() $f_3$
, which are each the negative of their
$f_3$
, which are each the negative of their
![]() $w_p$
-eigenvalue. The Atkin–Lehner correspondences
$w_p$
-eigenvalue. The Atkin–Lehner correspondences
![]() $w_p$
,
$w_p$
,
![]() $p\mid N$
, commute with the good Hecke correspondences
$p\mid N$
, commute with the good Hecke correspondences
![]() $T_n$
(i.e., with
$T_n$
(i.e., with
![]() $(n, N)=1$
), and this is sufficient for our purposes (see Remark 2.1). Assume that there exists
$(n, N)=1$
), and this is sufficient for our purposes (see Remark 2.1). Assume that there exists
![]() $p\mid N$
for which
$p\mid N$
for which
![]() $W_p(F)=-1$
. Using multiplicity one for newforms, this assumption can be parlayed into information about the torsion properties of the images of modified diagonal cycles under Abel–Jacobi maps, as long as one has sufficient understanding of the action of the Atkin–Lehner involution
$W_p(F)=-1$
. Using multiplicity one for newforms, this assumption can be parlayed into information about the torsion properties of the images of modified diagonal cycles under Abel–Jacobi maps, as long as one has sufficient understanding of the action of the Atkin–Lehner involution
![]() $w_p$
on the rational points of
$w_p$
on the rational points of
![]() $X_0(N)$
. The only rational points on composite level modular curves
$X_0(N)$
. The only rational points on composite level modular curves
![]() $X_0(N)$
of genus
$X_0(N)$
of genus
![]() $\geq 2$
are the rational cusps [Reference Kenku18]. It is known that the subgroup of the Jacobian
$\geq 2$
are the rational cusps [Reference Kenku18]. It is known that the subgroup of the Jacobian
![]() $J_0(N)$
generated by the cusps is torsion by the Manin–Drinfeld theorem [Reference Manin20]. It follows that Theorem 1.1 remains true for normalized newforms
$J_0(N)$
generated by the cusps is torsion by the Manin–Drinfeld theorem [Reference Manin20]. It follows that Theorem 1.1 remains true for normalized newforms
![]() $f_1,f_2,f_3$
of composite square-free level under the assumption
$f_1,f_2,f_3$
of composite square-free level under the assumption
![]() $W_p(F)=-1$
for some
$W_p(F)=-1$
for some
![]() $p\mid N$
.
$p\mid N$
.
The proof of Theorem 1.3 adapts verbatim to the setting of composite square-free level, provided that the eigenforms are newforms and
![]() $W_p(F)=-1$
for some
$W_p(F)=-1$
for some
![]() $p\mid N$
. This recovers [Reference Daub8, Theorem 3.3.8] by a different approach.
$p\mid N$
. This recovers [Reference Daub8, Theorem 3.3.8] by a different approach.
Examining Stein’s Table 2 in [Reference Darmon, Daub, Lichtenstein and Rotger5, Appendix], we obtain results similar to Theorem 1.2, e.g., in the following cases:
-
•
 $N=57$
: f corresponds to the elliptic curve with Cremona label
$N=57$
: f corresponds to the elliptic curve with Cremona label
 $57$
c, and g corresponds to the curves with labels
$57$
c, and g corresponds to the curves with labels
 $57$
a or
$57$
a or
 $57$
b.
$57$
b. -
•
 $N=58$
: f corresponds to the elliptic curve with Cremona label
$N=58$
: f corresponds to the elliptic curve with Cremona label
 $58$
b, and g corresponds to the curve with label
$58$
b, and g corresponds to the curve with label
 $58$
a.
$58$
a.
1.5 Related work
The approach taken in this paper is explicit and elementary, exploiting the connection between triple product root numbers and eigenvalues of Atkin–Lehner involutions. A more powerful approach is considered in the work of Yuan et al. [Reference Yuan, Zhang and Zhang28], using Prasad’s dichotomy for the existence of trilinear forms on automorphic representations. Forthcoming work of Qiu and Zhang [Reference Qiu and Zhang24] further develops this approach and gives applications.
1.6 Outline
Background on cusp forms of weight
![]() $2$
is recalled in Section 2. Section 3 recalls facts about the triple product L-function and states the Beilinson–Bloch conjecture in this setting. Section 4 constitutes the proof of Theorem 1.1. The application to Chow–Heegner points is given in Section 5. Theorem 1.2 is proved in Section 6.
$2$
is recalled in Section 2. Section 3 recalls facts about the triple product L-function and states the Beilinson–Bloch conjecture in this setting. Section 4 constitutes the proof of Theorem 1.1. The application to Chow–Heegner points is given in Section 5. Theorem 1.2 is proved in Section 6.
1.7 Notational conventions
Fix a complex embedding
![]() $\bar {\mathbb {Q}}\hookrightarrow \mathbb {C}$
, as well as p-adic embeddings
$\bar {\mathbb {Q}}\hookrightarrow \mathbb {C}$
, as well as p-adic embeddings
 $\bar {\mathbb {Q}}\hookrightarrow \mathbb {C}_p$
for each rational prime p. In this way, all finite extensions of
$\bar {\mathbb {Q}}\hookrightarrow \mathbb {C}_p$
for each rational prime p. In this way, all finite extensions of
![]() $\mathbb {Q}$
are viewed simultaneously as subfields of
$\mathbb {Q}$
are viewed simultaneously as subfields of
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $\mathbb {C}_p$
. For a field extension F of
$\mathbb {C}_p$
. For a field extension F of
![]() $\mathbb {Q}$
, the subscript F on a group (resp.
$\mathbb {Q}$
, the subscript F on a group (resp.
![]() $\mathbb {Q}$
-algebra) will denote the tensor product with F over
$\mathbb {Q}$
-algebra) will denote the tensor product with F over
![]() $\mathbb {Z}$
(resp.
$\mathbb {Z}$
(resp.
![]() $\mathbb {Q}$
). For any field K, we fix an algebraic closure
$\mathbb {Q}$
). For any field K, we fix an algebraic closure
![]() $\bar {K}$
. By a variety X over K, we shall mean an integral separated scheme of finite type over K. A subvariety is an integral separated closed subscheme. If F is a field extension of K,
$\bar {K}$
. By a variety X over K, we shall mean an integral separated scheme of finite type over K. A subvariety is an integral separated closed subscheme. If F is a field extension of K,
![]() $X_F$
will denote the base change of X to
$X_F$
will denote the base change of X to
![]() $\operatorname {\mathrm {Spec}}(F)$
. An algebraic cycle of codimension r on X is a finite
$\operatorname {\mathrm {Spec}}(F)$
. An algebraic cycle of codimension r on X is a finite
![]() $\mathbb {Z}$
-linear combination of subvarieties of
$\mathbb {Z}$
-linear combination of subvarieties of
![]() $X_{\bar {K}}$
of codimension r. The Chow group of codimension r algebraic cycles modulo
$X_{\bar {K}}$
of codimension r. The Chow group of codimension r algebraic cycles modulo
![]() $\bar {K}$
-rational equivalence will be denoted
$\bar {K}$
-rational equivalence will be denoted
![]() $\operatorname {\mathrm {CH}}^r(X)$
. It will be viewed as a functor from the category of field extension of K contained in
$\operatorname {\mathrm {CH}}^r(X)$
. It will be viewed as a functor from the category of field extension of K contained in
![]() $\bar {K}$
to the category of abelian groups given by the rule
$\bar {K}$
to the category of abelian groups given by the rule
This convention is borrowed from [Reference Darmon, Rotger and Sols7] and differs from the more classical notation of [Reference Fulton10]. Given two varieties X and Y over K, we write
![]() $\mathrm {Corr}^{r}(X, Y):=\operatorname {\mathrm {CH}}^{\dim X+r}(X\times Y)$
.
$\mathrm {Corr}^{r}(X, Y):=\operatorname {\mathrm {CH}}^{\dim X+r}(X\times Y)$
.
2 Cusp forms
Let
![]() $p> 3$
be a rational prime. Let
$p> 3$
be a rational prime. Let
![]() $Y:=Y_0(p)$
be the modular curve over
$Y:=Y_0(p)$
be the modular curve over
![]() $\mathbb {Q}$
for the congruence subgroup
$\mathbb {Q}$
for the congruence subgroup
![]() $\Gamma _0(p)\subset \mathrm { SL}_2(\mathbb {Z})$
consisting of matrices which are upper-triangular modulo p. It admits a canonical proper desingularization
$\Gamma _0(p)\subset \mathrm { SL}_2(\mathbb {Z})$
consisting of matrices which are upper-triangular modulo p. It admits a canonical proper desingularization
![]() $Y_0(p)\hookrightarrow X_0(p)$
, obtained over the complex numbers by adjoining the cusps. The curve
$Y_0(p)\hookrightarrow X_0(p)$
, obtained over the complex numbers by adjoining the cusps. The curve
![]() $X:=X_0(p)$
is a geometrically connected, smooth, and proper curve over
$X:=X_0(p)$
is a geometrically connected, smooth, and proper curve over
![]() $\mathbb {Q}$
. It is the coarse moduli scheme representing pairs
$\mathbb {Q}$
. It is the coarse moduli scheme representing pairs
![]() $(E, H)$
consisting of a generalized elliptic curve E over a
$(E, H)$
consisting of a generalized elliptic curve E over a
![]() $\mathbb {Q}$
-scheme S, together with a cyclic subgroup scheme H of order p. It admits a uniformization by the extended Poincaré upper half-plane
$\mathbb {Q}$
-scheme S, together with a cyclic subgroup scheme H of order p. It admits a uniformization by the extended Poincaré upper half-plane
which identifies
![]() $X(\mathbb {C})$
with the quotient
$X(\mathbb {C})$
with the quotient
![]() $\Gamma _0(p)\backslash \mathcal {H}^*$
. There are two cusps
$\Gamma _0(p)\backslash \mathcal {H}^*$
. There are two cusps
![]() $\xi _\infty $
and
$\xi _\infty $
and
![]() $\xi _0$
on X, which correspond via (2.1) to the points
$\xi _0$
on X, which correspond via (2.1) to the points
![]() $i\infty $
and
$i\infty $
and
![]() $0$
of
$0$
of
![]() $\mathcal {H}^*$
. The genus
$\mathcal {H}^*$
. The genus
![]() $g_X$
of X is given by the formula
$g_X$
of X is given by the formula
 $$ \begin{align} g_X= \begin{cases} \lfloor \frac{p+1}{12}\rfloor-1, & \text{ if } p\equiv 1 \pmod {12}, \\[6pt] \lfloor \frac{p+1}{12}\rfloor, & \text{ otherwise.} \end{cases} \end{align} $$
$$ \begin{align} g_X= \begin{cases} \lfloor \frac{p+1}{12}\rfloor-1, & \text{ if } p\equiv 1 \pmod {12}, \\[6pt] \lfloor \frac{p+1}{12}\rfloor, & \text{ otherwise.} \end{cases} \end{align} $$
The space
![]() $S_2(\Gamma _0(N))$
of weight
$S_2(\Gamma _0(N))$
of weight
![]() $2$
cusp forms of level
$2$
cusp forms of level
![]() $\Gamma _0(p)$
is naturally identified with the space of global sections of the sheaf of regular differential
$\Gamma _0(p)$
is naturally identified with the space of global sections of the sheaf of regular differential
![]() $1$
-forms on X via the isomorphism
$1$
-forms on X via the isomorphism
 $$ \begin{align} S_2(\Gamma_0(p))\overset{\sim}{{\longrightarrow}} H^0(X_{\mathbb{C}}, \Omega^1_{X}), \qquad f\mapsto \omega_f:=2\pi i f(\tau)d\tau. \end{align} $$
$$ \begin{align} S_2(\Gamma_0(p))\overset{\sim}{{\longrightarrow}} H^0(X_{\mathbb{C}}, \Omega^1_{X}), \qquad f\mapsto \omega_f:=2\pi i f(\tau)d\tau. \end{align} $$
In particular, the dimension of
![]() $S_2(\Gamma _0(p))$
is equal to
$S_2(\Gamma _0(p))$
is equal to
![]() $g_X$
.
$g_X$
.
2.1 Hecke operators
The curve X is equipped with the usual collection of Hecke correspondences, which act on cohomology and give rise to operators on
![]() $S_2(\Gamma _0(p))$
via (2.3). These correspondences and their induced operators are denoted by
$S_2(\Gamma _0(p))$
via (2.3). These correspondences and their induced operators are denoted by
![]() $U_p$
and
$U_p$
and
![]() $T_n$
, for integers
$T_n$
, for integers
![]() $n\geq 1$
coprime to p. Their precise definition can be found in [Reference Atkin and Lehner1, (3.1)].
$n\geq 1$
coprime to p. Their precise definition can be found in [Reference Atkin and Lehner1, (3.1)].
The curve X also comes equipped with the Atkin–Lehner involution
![]() $w_p$
. It is defined, following the moduli description, by mapping a p-isogeny
$w_p$
. It is defined, following the moduli description, by mapping a p-isogeny
![]() $\phi : E{\longrightarrow } E'$
of elliptic curves to its dual isogeny
$\phi : E{\longrightarrow } E'$
of elliptic curves to its dual isogeny
![]() $\phi ^\vee : E'{\longrightarrow } E$
. In terms of covering spaces, using (2.1), it is given by
$\phi ^\vee : E'{\longrightarrow } E$
. In terms of covering spaces, using (2.1), it is given by
 $\tau \mapsto -\frac {1}{p\tau }$
, where
$\tau \mapsto -\frac {1}{p\tau }$
, where
![]() $\tau \in \mathcal {H}$
. This involution is defined over
$\tau \in \mathcal {H}$
. This involution is defined over
![]() $\mathbb {Q}$
and thus maps
$\mathbb {Q}$
and thus maps
![]() $\mathbb {Q}$
-rational points of X to
$\mathbb {Q}$
-rational points of X to
![]() $\mathbb {Q}$
-rational points. It induces, via (2.3), an operator on
$\mathbb {Q}$
-rational points. It induces, via (2.3), an operator on
![]() $S_2(\Gamma _0(p))$
, which we also denote by
$S_2(\Gamma _0(p))$
, which we also denote by
![]() $w_p$
.
$w_p$
.
The operators
![]() $T_m$
, with
$T_m$
, with
![]() $(m, p)=1$
, on
$(m, p)=1$
, on
![]() $S_2(\Gamma _0(p))$
commute with the operators
$S_2(\Gamma _0(p))$
commute with the operators
![]() $T_n$
,
$T_n$
,
![]() $U_p$
and
$U_p$
and
![]() $w_p$
[Reference Atkin and Lehner1, Lemma 17]. Let
$w_p$
[Reference Atkin and Lehner1, Lemma 17]. Let
![]() $\mathbb {T}:=\mathbb {T}(p)$
denote the
$\mathbb {T}:=\mathbb {T}(p)$
denote the
![]() $\mathbb {Q}$
-algebra generated by the operators
$\mathbb {Q}$
-algebra generated by the operators
![]() $T_n$
, with
$T_n$
, with
![]() $(n,p)=1$
. The space of cusp forms
$(n,p)=1$
. The space of cusp forms
![]() $S_2(\Gamma _0(p))$
admits a basis of eigenforms for
$S_2(\Gamma _0(p))$
admits a basis of eigenforms for
![]() $\mathbb {T}$
[Reference Atkin and Lehner1, Theorem 2].
$\mathbb {T}$
[Reference Atkin and Lehner1, Theorem 2].
Let
![]() $f = \sum _{n\geq 1} a_n(f)q^n \in S_2(\Gamma _0(p))$
be a normalized eigenform, in the sense that
$f = \sum _{n\geq 1} a_n(f)q^n \in S_2(\Gamma _0(p))$
be a normalized eigenform, in the sense that
![]() $a_1(f)=1$
. Because the level is prime, there are no oldforms. As a consequence, we have the equality of operators
$a_1(f)=1$
. Because the level is prime, there are no oldforms. As a consequence, we have the equality of operators
![]() $U_p=-w_p$
. In particular, the operators
$U_p=-w_p$
. In particular, the operators
![]() $U_p$
and
$U_p$
and
![]() $w_p$
commute. Note that this is only the case for general composite level when restricting to newforms [Reference Atkin and Lehner1, Lemma 17]. It follows that
$w_p$
commute. Note that this is only the case for general composite level when restricting to newforms [Reference Atkin and Lehner1, Lemma 17]. It follows that
![]() $w_p(f)=-a_p(f)f$
. In particular, we have
$w_p(f)=-a_p(f)f$
. In particular, we have
![]() $a_p(f)\in \{ \pm 1 \}$
.
$a_p(f)\in \{ \pm 1 \}$
.
The normalized eigenform f determines a surjective homomorphism
![]() $\lambda _f : \mathbb {T} {\longrightarrow } K_f$
of algebras by sending
$\lambda _f : \mathbb {T} {\longrightarrow } K_f$
of algebras by sending
![]() $T_n$
to
$T_n$
to
![]() $a_n(f)$
. Here,
$a_n(f)$
. Here,
![]() $K_f$
is the totally real finite extension of
$K_f$
is the totally real finite extension of
![]() $\mathbb {Q}$
generated by the Fourier coefficients
$\mathbb {Q}$
generated by the Fourier coefficients
![]() $a_n(f)$
of f.
$a_n(f)$
of f.
Let
![]() $S_2(\Gamma _0(p))_f$
denote the f-isotypic component of
$S_2(\Gamma _0(p))_f$
denote the f-isotypic component of
![]() $S_2(\Gamma _0(p))$
consisting of cusp forms
$S_2(\Gamma _0(p))$
consisting of cusp forms
![]() $f'$
in
$f'$
in
![]() $S_2(\Gamma _0(p))$
such that
$S_2(\Gamma _0(p))$
such that
![]() $T(f')=\lambda _f(T) f'$
, for all
$T(f')=\lambda _f(T) f'$
, for all
![]() $T\in \mathbb {T}$
. By the theorem of multiplicity one [Reference Atkin and Lehner1, Lemma 20 and 21] of Atkin and Lehner for newforms, the space
$T\in \mathbb {T}$
. By the theorem of multiplicity one [Reference Atkin and Lehner1, Lemma 20 and 21] of Atkin and Lehner for newforms, the space
![]() $S_2(\Gamma _0(p))_f$
is one-dimensional over
$S_2(\Gamma _0(p))_f$
is one-dimensional over
![]() $\mathbb {C}$
. We have the spectral decomposition
$\mathbb {C}$
. We have the spectral decomposition
 $$\begin{align*}S_2(\Gamma_0(p)) = \bigoplus_{h} S_2(\Gamma_0(p))_h, \end{align*}$$
$$\begin{align*}S_2(\Gamma_0(p)) = \bigoplus_{h} S_2(\Gamma_0(p))_h, \end{align*}$$
where the sum is taken over all normalized eigenforms
![]() $h\in S_2(\Gamma _0(p))$
. Since the dual space
$h\in S_2(\Gamma _0(p))$
. Since the dual space
![]() $S_2(\Gamma _0(p))^\vee $
is a free
$S_2(\Gamma _0(p))^\vee $
is a free
![]() $\mathbb {T}_{\mathbb {C}}$
-module of rank one by multiplicity one, we similarly obtain a decomposition
$\mathbb {T}_{\mathbb {C}}$
-module of rank one by multiplicity one, we similarly obtain a decomposition
 $$\begin{align*}\mathbb{T}_{\mathbb{C}}=\bigoplus_h \mathbb{T}_{\mathbb{C}, h}, \end{align*}$$
$$\begin{align*}\mathbb{T}_{\mathbb{C}}=\bigoplus_h \mathbb{T}_{\mathbb{C}, h}, \end{align*}$$
where
![]() $\mathbb {T}_{\mathbb {C}, h}$
denotes the algebra of Hecke operators
$\mathbb {T}_{\mathbb {C}, h}$
denotes the algebra of Hecke operators
![]() $T_n$
, with
$T_n$
, with
![]() $(n, p)=1$
, acting on
$(n, p)=1$
, acting on
![]() $S_2(\Gamma _0(p))_h$
, which is again a
$S_2(\Gamma _0(p))_h$
, which is again a
![]() $\mathbb {C}$
-vector space of dimension one.
$\mathbb {C}$
-vector space of dimension one.
Let
![]() $[f]$
denote the
$[f]$
denote the
![]() $\mathrm {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})$
orbit of f. Form the complex vector space
$\mathrm {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})$
orbit of f. Form the complex vector space
![]() $\bigoplus _{g\in [f]} S_{2}(\Gamma _0(p))_g$
of dimension
$\bigoplus _{g\in [f]} S_{2}(\Gamma _0(p))_g$
of dimension
![]() $d_f:=[K_f : \mathbb {Q}]$
, and consider the
$d_f:=[K_f : \mathbb {Q}]$
, and consider the
![]() $\mathbb {Q}$
-subspace
$\mathbb {Q}$
-subspace
![]() $S_2(\Gamma _0(p))_{[f]}$
of forms with rational coefficients. This
$S_2(\Gamma _0(p))_{[f]}$
of forms with rational coefficients. This
![]() $\mathbb {Q}$
-vector space is stable under the action of
$\mathbb {Q}$
-vector space is stable under the action of
![]() $\mathbb {T}_{\mathbb {Q}}$
, and we let
$\mathbb {T}_{\mathbb {Q}}$
, and we let
![]() $\mathbb {T}_{\mathbb {Q}, [f]}$
denote the
$\mathbb {T}_{\mathbb {Q}, [f]}$
denote the
![]() $\mathbb {Q}$
-algebra generated by the Hecke operators acting on
$\mathbb {Q}$
-algebra generated by the Hecke operators acting on
![]() $S_2(\Gamma _0(p))_{[f]}$
. We then have the decomposition
$S_2(\Gamma _0(p))_{[f]}$
. We then have the decomposition
 $$ \begin{align} \mathbb{T}=\bigoplus_{[h]} \mathbb{T}_{\mathbb{Q}, [h]} \simeq \bigoplus_{[h]} K_h, \end{align} $$
$$ \begin{align} \mathbb{T}=\bigoplus_{[h]} \mathbb{T}_{\mathbb{Q}, [h]} \simeq \bigoplus_{[h]} K_h, \end{align} $$
where the sum is taken over all
![]() $\mathrm {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})$
conjugacy classes of normalized eigenforms in
$\mathrm {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})$
conjugacy classes of normalized eigenforms in
![]() $S_2(\Gamma _0(p))$
.
$S_2(\Gamma _0(p))$
.
Let
![]() $\operatorname {\mathrm {End}}_{\mathbb {Q}}(J)$
denote the ring of endomorphisms defined over
$\operatorname {\mathrm {End}}_{\mathbb {Q}}(J)$
denote the ring of endomorphisms defined over
![]() $\mathbb {Q}$
of the Jacobian variety
$\mathbb {Q}$
of the Jacobian variety
 $J:=\operatorname {\mathrm {Pic}}_{X/\mathbb {Q}}^0$
of X, and let
$J:=\operatorname {\mathrm {Pic}}_{X/\mathbb {Q}}^0$
of X, and let
 $\operatorname {\mathrm {End}}_{\mathbb {Q}}^0(J):=\operatorname {\mathrm {End}}_{\mathbb {Q}}(J)\otimes \mathbb {Q}$
. As p is prime, we have
$\operatorname {\mathrm {End}}_{\mathbb {Q}}^0(J):=\operatorname {\mathrm {End}}_{\mathbb {Q}}(J)\otimes \mathbb {Q}$
. As p is prime, we have
 $\operatorname {\mathrm {End}}_{\mathbb {Q}}^0(J)= \mathbb {T}$
[Reference Ribet25, Corollary 3.3]. To summarize, we have the decomposition
$\operatorname {\mathrm {End}}_{\mathbb {Q}}^0(J)= \mathbb {T}$
[Reference Ribet25, Corollary 3.3]. To summarize, we have the decomposition
 $$ \begin{align} \operatorname{\mathrm{End}}_{\mathbb{Q}}^0(J)= \mathbb{T}\simeq \bigoplus_{[h]} K_h. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{End}}_{\mathbb{Q}}^0(J)= \mathbb{T}\simeq \bigoplus_{[h]} K_h. \end{align} $$
It will be useful to remark that there is a natural ring isomorphism
 $$ \begin{align} \operatorname{\mathrm{End}}_{\mathbb{Q}}^0(J)\simeq (\operatorname{\mathrm{CH}}^1(X^2)(\mathbb{Q})_{\mathbb{Q}})/(\operatorname{\mathrm{pr}}_1^* \operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})_{\mathbb{Q}}+\operatorname{\mathrm{pr}}_2^* \operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})_{\mathbb{Q}}), \end{align} $$
$$ \begin{align} \operatorname{\mathrm{End}}_{\mathbb{Q}}^0(J)\simeq (\operatorname{\mathrm{CH}}^1(X^2)(\mathbb{Q})_{\mathbb{Q}})/(\operatorname{\mathrm{pr}}_1^* \operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})_{\mathbb{Q}}+\operatorname{\mathrm{pr}}_2^* \operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})_{\mathbb{Q}}), \end{align} $$
by [Reference Birkenhake and Lange3, Theorem 11.5.1]. See Section 1.7 for our conventions about Chow groups.
Remark 2.1 The exposition is simplified by the assumption that the level is prime, which implies that there are no oldforms. We refer to [Reference Darmon, Diamond and Taylor6, Section 1.6] for the decomposition (2.4) in the more general setting of composite level N. In this case, the algebra
 $\operatorname {\mathrm {End}}^0_{\mathbb {Q}}(J)$
is a product of matrix algebras. It contains
$\operatorname {\mathrm {End}}^0_{\mathbb {Q}}(J)$
is a product of matrix algebras. It contains
![]() $\mathbb {T}$
as its center and the full Hecke algebra as a maximal commutative subalgebra. Moreover,
$\mathbb {T}$
as its center and the full Hecke algebra as a maximal commutative subalgebra. Moreover,
 $\operatorname {\mathrm {End}}^0_{\mathbb {Q}}(J)$
is generated as a
$\operatorname {\mathrm {End}}^0_{\mathbb {Q}}(J)$
is generated as a
![]() $\mathbb {Q}$
-algebra by
$\mathbb {Q}$
-algebra by
![]() $\mathbb {T}$
, together with certain degeneracy operators [Reference Kani17, Theorem 1].
$\mathbb {T}$
, together with certain degeneracy operators [Reference Kani17, Theorem 1].
2.2 Hecke projectors
Let
![]() $f = \sum _{n\geq 1} a_n(f)q^n \in S_2(\Gamma _0(p))$
be a normalized eigenform. Let
$f = \sum _{n\geq 1} a_n(f)q^n \in S_2(\Gamma _0(p))$
be a normalized eigenform. Let
![]() $V:=S_2(\Gamma _0(p))^\vee $
be the
$V:=S_2(\Gamma _0(p))^\vee $
be the
![]() $\mathbb {C}$
-dual of
$\mathbb {C}$
-dual of
![]() $S_2(\Gamma _0(p))$
. The complex points of the Jacobian
$S_2(\Gamma _0(p))$
. The complex points of the Jacobian
![]() $J_{\mathbb {C}}$
are
$J_{\mathbb {C}}$
are
where
![]() $\Lambda :=\operatorname {\mathrm {Im}} H_{1}(X_{\mathbb {C}}(\mathbb {C}), \mathbb {Z})$
is viewed as a lattice via integration of differential forms. By (2.3), we thus have an identification
$\Lambda :=\operatorname {\mathrm {Im}} H_{1}(X_{\mathbb {C}}(\mathbb {C}), \mathbb {Z})$
is viewed as a lattice via integration of differential forms. By (2.3), we thus have an identification
![]() $J_{\mathbb {C}}(\mathbb {C})=V/\Lambda $
as a
$J_{\mathbb {C}}(\mathbb {C})=V/\Lambda $
as a
![]() $g_X$
-dimensional complex torus, where we recall that
$g_X$
-dimensional complex torus, where we recall that
![]() $g_X$
is the genus of X. Let
$g_X$
is the genus of X. Let
![]() $V_f$
be the subspace of V on which
$V_f$
be the subspace of V on which
![]() $\mathbb {T}$
acts via the homomorphism
$\mathbb {T}$
acts via the homomorphism
![]() $\lambda _f : \mathbb {T} {\longrightarrow } K_f$
, and let
$\lambda _f : \mathbb {T} {\longrightarrow } K_f$
, and let
![]() $\operatorname {\mathrm {pr}}_f : V{\longrightarrow } V_f$
be the orthogonal projection with respect to the Petersson scalar product. The projector
$\operatorname {\mathrm {pr}}_f : V{\longrightarrow } V_f$
be the orthogonal projection with respect to the Petersson scalar product. The projector
![]() $\operatorname {\mathrm {pr}}_f$
naturally belongs to
$\operatorname {\mathrm {pr}}_f$
naturally belongs to
![]() $\mathbb {T}_{K_f}=\mathbb {T}\otimes _{\mathbb {Q}} K_f$
, and by (2.5) and (2.6) we may view
$\mathbb {T}_{K_f}=\mathbb {T}\otimes _{\mathbb {Q}} K_f$
, and by (2.5) and (2.6) we may view
![]() $\operatorname {\mathrm {pr}}_f$
as an idempotent element
$\operatorname {\mathrm {pr}}_f$
as an idempotent element
 $$ \begin{align} [t_f] \in (\operatorname{\mathrm{CH}}^1(X^2)(\mathbb{Q})_{K_f})/(\operatorname{\mathrm{pr}}_1^* \operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})_{K_f}+\operatorname{\mathrm{pr}}_2^* \operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})_{K_f}), \end{align} $$
$$ \begin{align} [t_f] \in (\operatorname{\mathrm{CH}}^1(X^2)(\mathbb{Q})_{K_f})/(\operatorname{\mathrm{pr}}_1^* \operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})_{K_f}+\operatorname{\mathrm{pr}}_2^* \operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})_{K_f}), \end{align} $$
where
![]() $t_f$
denotes some lift of
$t_f$
denotes some lift of
![]() $\operatorname {\mathrm {pr}}_f$
to
$\operatorname {\mathrm {pr}}_f$
to
 $\operatorname {\mathrm {CH}}^1(X^2)(\mathbb {Q})_{K_f}$
. The correspondence
$\operatorname {\mathrm {CH}}^1(X^2)(\mathbb {Q})_{K_f}$
. The correspondence
![]() $t_f$
is some choice of
$t_f$
is some choice of
![]() $K_f$
-linear combination of Hecke correspondences which induces the projection on cohomology onto the f-isotypic component.
$K_f$
-linear combination of Hecke correspondences which induces the projection on cohomology onto the f-isotypic component.
If we let
![]() $V_{[f]}:=\bigoplus _{g\in [f]} V_g$
and
$V_{[f]}:=\bigoplus _{g\in [f]} V_g$
and
![]() $\operatorname {\mathrm {pr}}_{[f]}:=\sum _{g\in [f]} \operatorname {\mathrm {pr}}_g$
, then
$\operatorname {\mathrm {pr}}_{[f]}:=\sum _{g\in [f]} \operatorname {\mathrm {pr}}_g$
, then
![]() $\operatorname {\mathrm {pr}}_{[f]}$
is the orthogonal projection
$\operatorname {\mathrm {pr}}_{[f]}$
is the orthogonal projection
![]() $V{\longrightarrow } V_{[f]}$
with respect to the Petersson scalar product. Note that
$V{\longrightarrow } V_{[f]}$
with respect to the Petersson scalar product. Note that
![]() $\operatorname {\mathrm {pr}}_{[f]}$
naturally belongs to the Hecke algebra
$\operatorname {\mathrm {pr}}_{[f]}$
naturally belongs to the Hecke algebra
![]() $\mathbb {T}$
, and corresponds under (2.5) to the idempotent element
$\mathbb {T}$
, and corresponds under (2.5) to the idempotent element
![]() $e_{[f]}$
in
$e_{[f]}$
in
![]() $\bigoplus _{[h]} K_h$
which has
$\bigoplus _{[h]} K_h$
which has
![]() $1$
as
$1$
as
![]() $[f]$
-coordinate and
$[f]$
-coordinate and
![]() $0$
as
$0$
as
![]() $[h]$
-coordinate for
$[h]$
-coordinate for
![]() $[h]\neq [f]$
. By (2.6), we may view
$[h]\neq [f]$
. By (2.6), we may view
![]() $\operatorname {\mathrm {pr}}_{[f]}$
as an idempotent element
$\operatorname {\mathrm {pr}}_{[f]}$
as an idempotent element
 $$ \begin{align} [t_{[f]}] \in (\operatorname{\mathrm{CH}}^1(X^2)(\mathbb{Q})_{\mathbb{Q}})/(\operatorname{\mathrm{pr}}_1^* \operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})_{\mathbb{Q}}+\operatorname{\mathrm{pr}}_2^* \operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})_{\mathbb{Q}}), \end{align} $$
$$ \begin{align} [t_{[f]}] \in (\operatorname{\mathrm{CH}}^1(X^2)(\mathbb{Q})_{\mathbb{Q}})/(\operatorname{\mathrm{pr}}_1^* \operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})_{\mathbb{Q}}+\operatorname{\mathrm{pr}}_2^* \operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})_{\mathbb{Q}}), \end{align} $$
where
![]() $t_{[f]}$
denotes some lift of
$t_{[f]}$
denotes some lift of
![]() $\operatorname {\mathrm {pr}}_{[f]}$
to
$\operatorname {\mathrm {pr}}_{[f]}$
to
 $\operatorname {\mathrm {CH}}^1(X^2)(\mathbb {Q})_{\mathbb {Q}}$
.
$\operatorname {\mathrm {CH}}^1(X^2)(\mathbb {Q})_{\mathbb {Q}}$
.
Let
![]() $I_f$
be the ideal
$I_f$
be the ideal
![]() $\ker (\lambda _f)\cap \mathbb {T}_{\mathbb {Z}}$
of the integral Hecke algebra
$\ker (\lambda _f)\cap \mathbb {T}_{\mathbb {Z}}$
of the integral Hecke algebra
![]() $\mathbb {T}_{\mathbb {Z}}$
(the
$\mathbb {T}_{\mathbb {Z}}$
(the
![]() $\mathbb {Z}$
-algebra generated by the Hecke operators
$\mathbb {Z}$
-algebra generated by the Hecke operators
![]() $T_n$
, with
$T_n$
, with
![]() $(n,p)=1$
). The image
$(n,p)=1$
). The image
![]() $I_f(J)$
is a subabelian variety which is stable under
$I_f(J)$
is a subabelian variety which is stable under
![]() $\mathbb {T}_{\mathbb {Z}}$
and defined over
$\mathbb {T}_{\mathbb {Z}}$
and defined over
![]() $\mathbb {Q}$
. The abelian variety associated with the Galois orbit
$\mathbb {Q}$
. The abelian variety associated with the Galois orbit
![]() $[f]$
by Eichler and Shimura [Reference Shimura27] is defined as the quotient
$[f]$
by Eichler and Shimura [Reference Shimura27] is defined as the quotient
![]() $A_{[f]}:=J/I_f(J)$
. Let
$A_{[f]}:=J/I_f(J)$
. Let
![]() $m_{[f]}\in \mathbb {N}$
be the denominator of
$m_{[f]}\in \mathbb {N}$
be the denominator of
![]() $\operatorname {\mathrm {pr}}_{[f]}\in \mathbb {T}$
, i.e., the smallest positive integer such that
$\operatorname {\mathrm {pr}}_{[f]}\in \mathbb {T}$
, i.e., the smallest positive integer such that
![]() $\pi _{[f]}:=m_{[f]}\operatorname {\mathrm {pr}}_{[f]}$
belongs to
$\pi _{[f]}:=m_{[f]}\operatorname {\mathrm {pr}}_{[f]}$
belongs to
![]() $\mathbb {T}_{\mathbb {Z}}$
. Then
$\mathbb {T}_{\mathbb {Z}}$
. Then
![]() $A_{[f]}$
is isomorphic over
$A_{[f]}$
is isomorphic over
![]() $\mathbb {C}$
to the complex torus
$\mathbb {C}$
to the complex torus
![]() $V_{[f]}/\pi _{[f]}(\Lambda )$
, and the map
$V_{[f]}/\pi _{[f]}(\Lambda )$
, and the map
![]() $\pi _{[f]} : V/\Lambda {\longrightarrow } V_{[f]}/\pi _{[f]}(\Lambda )$
corresponds to the natural quotient map
$\pi _{[f]} : V/\Lambda {\longrightarrow } V_{[f]}/\pi _{[f]}(\Lambda )$
corresponds to the natural quotient map
![]() $\pi _{[f]}:J{\longrightarrow } A_{[f]}$
of abelian varieties over
$\pi _{[f]}:J{\longrightarrow } A_{[f]}$
of abelian varieties over
![]() $\mathbb {Q}$
with kernel
$\mathbb {Q}$
with kernel
![]() $I_f(J)$
[Reference Darmon, Diamond and Taylor6, Lemma 1.46].
$I_f(J)$
[Reference Darmon, Diamond and Taylor6, Lemma 1.46].
3 Triple products
Let
![]() $ f_1=\sum _{n\geq 1} a_n(f_1)q^n, f_2=\sum _{n\geq 1} a_n(f_2)q^n,$
and
$ f_1=\sum _{n\geq 1} a_n(f_1)q^n, f_2=\sum _{n\geq 1} a_n(f_2)q^n,$
and
![]() $f_3=\sum _{n\geq 1} a_n(f_3)q^n $
be three normalized cuspidal eigenforms of weight
$f_3=\sum _{n\geq 1} a_n(f_3)q^n $
be three normalized cuspidal eigenforms of weight
![]() $2$
and level
$2$
and level
![]() $\Gamma _0(p)$
, and let
$\Gamma _0(p)$
, and let
![]() $F:=f_1\otimes f_2\otimes f_3$
be the associated cusp form of weight
$F:=f_1\otimes f_2\otimes f_3$
be the associated cusp form of weight
![]() $(2, 2, 2)$
for
$(2, 2, 2)$
for
![]() $\Gamma _0(p)^3$
. Let
$\Gamma _0(p)^3$
. Let
![]() $K_F = K_{f_1}\cdot K_{f_2} \cdot K_{f_3}$
denote the compositum of the Hecke fields of the forms
$K_F = K_{f_1}\cdot K_{f_2} \cdot K_{f_3}$
denote the compositum of the Hecke fields of the forms
![]() $f_1, f_2,$
and
$f_1, f_2,$
and
![]() $f_3$
.
$f_3$
.
3.1 Triple product L-functions
For
![]() $i\in \{ 1,2,3 \}$
and a prime
$i\in \{ 1,2,3 \}$
and a prime
![]() $\ell $
, let
$\ell $
, let
![]() $\lambda _i$
be the prime ideal of
$\lambda _i$
be the prime ideal of
![]() $K_{f_i}$
above
$K_{f_i}$
above
![]() $\ell $
determined by the embeddings fixed in Section 1.7. Denote by
$\ell $
determined by the embeddings fixed in Section 1.7. Denote by
![]() $K_{f_i,\lambda _i}$
the completion of
$K_{f_i,\lambda _i}$
the completion of
![]() $K_{f_i}$
with respect to
$K_{f_i}$
with respect to
![]() $\lambda _i$
, and let
$\lambda _i$
, and let
 $ V_\ell (f_i) : \mathrm {Gal}(\bar {\mathbb {Q}}/\mathbb {Q}) {\longrightarrow } \mathbf {GL}_2(K_{f_i, \lambda _i}) $
be the two-dimensional
$ V_\ell (f_i) : \mathrm {Gal}(\bar {\mathbb {Q}}/\mathbb {Q}) {\longrightarrow } \mathbf {GL}_2(K_{f_i, \lambda _i}) $
be the two-dimensional
![]() $\ell $
-adic Galois representation associated to
$\ell $
-adic Galois representation associated to
![]() $f_i$
[Reference Darmon, Diamond and Taylor6, Theorem 3.1]. We remark that given any choice of correspondence
$f_i$
[Reference Darmon, Diamond and Taylor6, Theorem 3.1]. We remark that given any choice of correspondence
![]() $t_{f_i}$
as in (2.7), the representation
$t_{f_i}$
as in (2.7), the representation
![]() $V_\ell (f_i)$
admits a description as
$V_\ell (f_i)$
admits a description as
 $ (t_{f_i})_*H^1_{\operatorname {\mathrm {et}}}(X_{\bar {\mathbb {Q}}}, \mathbb {Q}_\ell ) $
followed by the map induced by the projection
$ (t_{f_i})_*H^1_{\operatorname {\mathrm {et}}}(X_{\bar {\mathbb {Q}}}, \mathbb {Q}_\ell ) $
followed by the map induced by the projection
![]() $K_{f_i}\otimes \mathbb {Q}_\ell {\longrightarrow } K_{f_i,\lambda _i}$
.
$K_{f_i}\otimes \mathbb {Q}_\ell {\longrightarrow } K_{f_i,\lambda _i}$
.
The triple product L-function
![]() $L(F,s)=L(f_1, f_2, f_3, s)$
is the L-function associated with the compatible family of eight-dimensional
$L(F,s)=L(f_1, f_2, f_3, s)$
is the L-function associated with the compatible family of eight-dimensional
![]() $\ell $
-adic representations
$\ell $
-adic representations
It admits a description as an Euler product converging absolutely for
![]() $\mathscr{R} (s)>5/2$
. The Euler factors are given explicitly in [Reference Gross and Kudla11, (1.7) and (1.8)].
$\mathscr{R} (s)>5/2$
. The Euler factors are given explicitly in [Reference Gross and Kudla11, (1.7) and (1.8)].
Define the local L-factor at infinity following the general recipe of [Reference Deligne9] by
The completed L-function
![]() $\Lambda ^*(F, s):=(p^5)^{\frac {s}{2}}L_\infty (F, s)L(F,s)$
admits an analytic continuation to the entire complex plane and satisfies the functional equation
$\Lambda ^*(F, s):=(p^5)^{\frac {s}{2}}L_\infty (F, s)L(F,s)$
admits an analytic continuation to the entire complex plane and satisfies the functional equation
where
![]() $W(F)\in \{ \pm 1 \}$
is the global root number of F [Reference Gross and Kudla11, Proposition 1.1]. The global root number, as stated in [Reference Gross and Kudla11, Section 1], is given by
$W(F)\in \{ \pm 1 \}$
is the global root number of F [Reference Gross and Kudla11, Proposition 1.1]. The global root number, as stated in [Reference Gross and Kudla11, Section 1], is given by
A detailed proof of this can for instance be found in [Reference Lilienfeldt19, Proposition 4.5].
3.2 The Beilinson–Bloch conjecture
The center of symmetry of the functional equation (3.1) is the point
![]() $s=2$
at which
$s=2$
at which
![]() $L(F, s)$
has no pole. Moreover,
$L(F, s)$
has no pole. Moreover,
![]() $L_\infty (F, s)$
has neither zero nor pole at
$L_\infty (F, s)$
has neither zero nor pole at
![]() $s=2$
, so the center is a critical point, and we have
$s=2$
, so the center is a critical point, and we have
 $$ \begin{align} W(F)=(-1)^{\operatorname{\mathrm{ord}}_{s=2} L(F, s)}. \end{align} $$
$$ \begin{align} W(F)=(-1)^{\operatorname{\mathrm{ord}}_{s=2} L(F, s)}. \end{align} $$
For
![]() $i\in \{ 1,2,3 \}$
, let
$i\in \{ 1,2,3 \}$
, let
![]() $t_{f_i}$
be a choice of self-correspondence of X lifting the
$t_{f_i}$
be a choice of self-correspondence of X lifting the
![]() $f_i$
-Hecke projector
$f_i$
-Hecke projector
![]() $\operatorname {\mathrm {pr}}_{f_i}$
(2.7). Define a self-correspondence of
$\operatorname {\mathrm {pr}}_{f_i}$
(2.7). Define a self-correspondence of
![]() $X^3$
by
$X^3$
by
 $$ \begin{align} t_F := t_{f_1} \otimes t_{f_2} \otimes t_{f_3}=\operatorname{\mathrm{pr}}_{14}^*(t_{f_1}) \cdot \operatorname{\mathrm{pr}}_{25}^*(t_{f_2})\cdot \operatorname{\mathrm{pr}}_{36}^*(t_{f_3}) \in \mathrm{Corr}^0(X^3, X^3)(\mathbb{Q})_{K_F}, \end{align} $$
$$ \begin{align} t_F := t_{f_1} \otimes t_{f_2} \otimes t_{f_3}=\operatorname{\mathrm{pr}}_{14}^*(t_{f_1}) \cdot \operatorname{\mathrm{pr}}_{25}^*(t_{f_2})\cdot \operatorname{\mathrm{pr}}_{36}^*(t_{f_3}) \in \mathrm{Corr}^0(X^3, X^3)(\mathbb{Q})_{K_F}, \end{align} $$
where
 $\operatorname {\mathrm {pr}}_{ij} : X^6 {\longrightarrow } X^2$
denotes the natural projection to the ith and jth components.
$\operatorname {\mathrm {pr}}_{ij} : X^6 {\longrightarrow } X^2$
denotes the natural projection to the ith and jth components.
Remark 3.1 The correspondence
![]() $t_F$
is some choice of
$t_F$
is some choice of
![]() $K_F$
-linear combination of tensor products of Hecke correspondences projecting to the
$K_F$
-linear combination of tensor products of Hecke correspondences projecting to the
![]() $1$
-dimensional F-isotypic component of the
$1$
-dimensional F-isotypic component of the
![]() $(\mathbb {T}^{\otimes 3}\otimes \mathbb {R})$
-module
$(\mathbb {T}^{\otimes 3}\otimes \mathbb {R})$
-module
![]() $H^0(X^3, \Omega ^3_{X^3})\otimes \mathbb {R}=H^0(X, \Omega ^1_{X})^{\otimes 3} \otimes \mathbb {R}$
.
$H^0(X^3, \Omega ^3_{X^3})\otimes \mathbb {R}=H^0(X, \Omega ^1_{X})^{\otimes 3} \otimes \mathbb {R}$
.
The Beilinson–Bloch conjecture [Reference Bloch4] predicts in this setting that
In the case when
![]() $W(F)=+1$
, Gross and Kudla proved a formula for the central value
$W(F)=+1$
, Gross and Kudla proved a formula for the central value
![]() $L(F,2)$
, expressing it as a product of a complex period and an algebraic number [Reference Gross and Kudla11, Proposition 10.8]. This algebraic number admits an explicit description in terms of the coefficients of the Jacquet–Langlands transfers of
$L(F,2)$
, expressing it as a product of a complex period and an algebraic number [Reference Gross and Kudla11, Proposition 10.8]. This algebraic number admits an explicit description in terms of the coefficients of the Jacquet–Langlands transfers of
![]() $f_1, f_2,$
and
$f_1, f_2,$
and
![]() $f_3$
to the definite quaternion algebra ramified at p and
$f_3$
to the definite quaternion algebra ramified at p and
![]() $\infty $
.
$\infty $
.
In the case when
![]() $W(F)=-1$
, the L-function
$W(F)=-1$
, the L-function
![]() $L(F, s)$
vanishes to odd order at its centre
$L(F, s)$
vanishes to odd order at its centre
![]() $s=2$
. By (3.5), we expect
$s=2$
. By (3.5), we expect
![]() $(t_F)_*(\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})_{K_F})$
to have dimension greater or equal to
$(t_F)_*(\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})_{K_F})$
to have dimension greater or equal to
![]() $1$
. A natural element of
$1$
. A natural element of
![]() $\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})$
to consider is the modified diagonal cycle, also referred to as the Gross–Kudla–Schoen cycle, which we now define.
$\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})$
to consider is the modified diagonal cycle, also referred to as the Gross–Kudla–Schoen cycle, which we now define.
Let
![]() $\Delta $
denote the image of X under the diagonal embedding
$\Delta $
denote the image of X under the diagonal embedding
![]() $X{\longrightarrow } X^3$
, i.e.,
$X{\longrightarrow } X^3$
, i.e.,
In order to get a null-homologous cycle, we apply a projector to
![]() $\Delta $
following [Reference Gross and Kudla11, Reference Gross and Schoen12].
$\Delta $
following [Reference Gross and Kudla11, Reference Gross and Schoen12].
Definition 3.1 Let C be a smooth, projective, and geometrically connected curve over a number field k, and let e be a point in
![]() $X(\bar {k})$
. For any nonempty subset T of
$X(\bar {k})$
. For any nonempty subset T of
![]() $\{ 1, 2, 3 \}$
, let
$\{ 1, 2, 3 \}$
, let
![]() $T'$
denote the complementary set. Write
$T'$
denote the complementary set. Write
![]() $p_T : C^3{\longrightarrow } C^{\vert T \vert }$
for the natural projection map and let
$p_T : C^3{\longrightarrow } C^{\vert T \vert }$
for the natural projection map and let
![]() $q_T(e) : C^{\vert T\vert }{\longrightarrow } C^3$
denote the inclusion obtained by filling in the missing coordinates using the point e. Let
$q_T(e) : C^{\vert T\vert }{\longrightarrow } C^3$
denote the inclusion obtained by filling in the missing coordinates using the point e. Let
![]() $P_{T}(e)$
denote the graph of
$P_{T}(e)$
denote the graph of
![]() $q_{T}(e)\circ p_T$
viewed as a codimension
$q_{T}(e)\circ p_T$
viewed as a codimension
![]() $3$
cycle on the product
$3$
cycle on the product
![]() $C^3\times C^3$
. Define the Gross–Kudla–Schoen projector
$C^3\times C^3$
. Define the Gross–Kudla–Schoen projector
 $$\begin{align*}P_{\operatorname{\mathrm{GKS}}}(e):=\sum_T (-1)^{\vert T'\vert} P_T(e) \in \operatorname{\mathrm{CH}}^3(C^3\times C^3)(\bar{k}), \end{align*}$$
$$\begin{align*}P_{\operatorname{\mathrm{GKS}}}(e):=\sum_T (-1)^{\vert T'\vert} P_T(e) \in \operatorname{\mathrm{CH}}^3(C^3\times C^3)(\bar{k}), \end{align*}$$
where the sum is taken over all subsets of
![]() $\{ 1, 2, 3 \}$
. This is an idempotent in the ring of correspondences of
$\{ 1, 2, 3 \}$
. This is an idempotent in the ring of correspondences of
![]() $C^3$
with the property that it annihilates the cohomology groups
$C^3$
with the property that it annihilates the cohomology groups
![]() $H^{i}(C_{\mathbb {C}}^3(\mathbb {C}), \mathbb {Z})$
, for
$H^{i}(C_{\mathbb {C}}^3(\mathbb {C}), \mathbb {Z})$
, for
![]() $i\in \{ 4,5,6 \}$
, and maps
$i\in \{ 4,5,6 \}$
, and maps
![]() $H^3(C_{\mathbb {C}}^3(\mathbb {C}), \mathbb {Z})$
onto the Künneth summand
$H^3(C_{\mathbb {C}}^3(\mathbb {C}), \mathbb {Z})$
onto the Künneth summand
![]() $H^1(C_{\mathbb {C}}(\mathbb {C}), \mathbb {Z})^{\otimes 3}$
[Reference Gross and Schoen12, Corollary 2.6].
$H^1(C_{\mathbb {C}}(\mathbb {C}), \mathbb {Z})^{\otimes 3}$
[Reference Gross and Schoen12, Corollary 2.6].
Given a point
![]() $e\in X(\bar {\mathbb {Q}})$
, the Gross–Kudla–Schoen cycle with base point e is
$e\in X(\bar {\mathbb {Q}})$
, the Gross–Kudla–Schoen cycle with base point e is
Note that the cycle
![]() $\Delta _{\operatorname {\mathrm {GKS}}}(e)$
is in fact null-homologous since
$\Delta _{\operatorname {\mathrm {GKS}}}(e)$
is in fact null-homologous since
![]() $P_{\operatorname {\mathrm {GKS}}}(e)$
annihilates
$P_{\operatorname {\mathrm {GKS}}}(e)$
annihilates
![]() $H^4(X_{\mathbb {C}}^3 (\mathbb {C}), \mathbb {Z})$
, the target of the cycle class map. Define the “F-isotypic component” of the Gross–Kudla–Schoen cycle by
$H^4(X_{\mathbb {C}}^3 (\mathbb {C}), \mathbb {Z})$
, the target of the cycle class map. Define the “F-isotypic component” of the Gross–Kudla–Schoen cycle by
![]() $(t_F)_*\Delta _{\operatorname {\mathrm {GKS}}}(e)\in \operatorname {\mathrm {CH}}^2(X^3)_0(\bar {\mathbb {Q}})_{K_F}$
.
$(t_F)_*\Delta _{\operatorname {\mathrm {GKS}}}(e)\in \operatorname {\mathrm {CH}}^2(X^3)_0(\bar {\mathbb {Q}})_{K_F}$
.
Remark 3.2 Although
![]() $t_F$
is not unique, the difference
$t_F$
is not unique, the difference
![]() $t_F-t_F'$
of two such projectors annihilates
$t_F-t_F'$
of two such projectors annihilates
![]() $H^0(X^3_{\mathbb {C}}, \Omega ^3_{X^3})$
. Conditional on the nondegeneracy of the Beilinson–Bloch height pairing for
$H^0(X^3_{\mathbb {C}}, \Omega ^3_{X^3})$
. Conditional on the nondegeneracy of the Beilinson–Bloch height pairing for
![]() $X^2$
, this implies that
$X^2$
, this implies that
![]() $(t_F)_*\Delta _{\operatorname {\mathrm {GKS}}}(e)=(t_F')_*\Delta _{\operatorname {\mathrm {GKS}}}(e)$
. Unconditionally, the Beilinson–Bloch height of
$(t_F)_*\Delta _{\operatorname {\mathrm {GKS}}}(e)=(t_F')_*\Delta _{\operatorname {\mathrm {GKS}}}(e)$
. Unconditionally, the Beilinson–Bloch height of
![]() $(t_F)_*\Delta _{\operatorname {\mathrm {GKS}}}(e)$
is independent of the choice of
$(t_F)_*\Delta _{\operatorname {\mathrm {GKS}}}(e)$
is independent of the choice of
![]() $t_F$
[Reference Gross and Schoen12, Proposition 8.3, Notes 8.5 and 8.6].
$t_F$
[Reference Gross and Schoen12, Proposition 8.3, Notes 8.5 and 8.6].
Gross and Kudla [Reference Gross and Kudla11, Conjecture 13.2] conjectured the formula
 $$ \begin{align} \frac{L'(F, 2)}{\Omega_F} = \langle (t_F)_* (\Delta_{\operatorname{\mathrm{GKS}}}(\xi_\infty)), (t_F)_* (\Delta_{\operatorname{\mathrm{GKS}}}(\xi_\infty)) \rangle^{\mathrm{BB}}, \end{align} $$
$$ \begin{align} \frac{L'(F, 2)}{\Omega_F} = \langle (t_F)_* (\Delta_{\operatorname{\mathrm{GKS}}}(\xi_\infty)), (t_F)_* (\Delta_{\operatorname{\mathrm{GKS}}}(\xi_\infty)) \rangle^{\mathrm{BB}}, \end{align} $$
where
![]() $\langle \: , \: \rangle ^{\mathrm {BB}} : \operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})_{\mathbb {R}} \times \operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})_{\mathbb {R}} {\longrightarrow } \mathbb {R}$
denotes the Beilinson–Bloch height pairing [Reference Gross and Kudla11, (13.9)], and
$\langle \: , \: \rangle ^{\mathrm {BB}} : \operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})_{\mathbb {R}} \times \operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})_{\mathbb {R}} {\longrightarrow } \mathbb {R}$
denotes the Beilinson–Bloch height pairing [Reference Gross and Kudla11, (13.9)], and
 $ \Omega _{F}:=\Vert \omega _{f_1} \Vert ^2\cdot \Vert \omega _{f_2} \Vert ^2\cdot \Vert \omega _{f_3} \Vert ^2/(4\pi p) $
is the complex period of F with
$ \Omega _{F}:=\Vert \omega _{f_1} \Vert ^2\cdot \Vert \omega _{f_2} \Vert ^2\cdot \Vert \omega _{f_3} \Vert ^2/(4\pi p) $
is the complex period of F with
![]() $\Vert \cdot \Vert $
denoting the Petersson norm. A proof of (3.8) due to Yuan et al. was announced in [Reference Yuan, Zhang and Zhang28].
$\Vert \cdot \Vert $
denoting the Petersson norm. A proof of (3.8) due to Yuan et al. was announced in [Reference Yuan, Zhang and Zhang28].
4 Abel–Jacobi maps
Let
![]() $f_1, f_2, f_3$
be three normalized eigenforms in
$f_1, f_2, f_3$
be three normalized eigenforms in
![]() $S_2(\Gamma _0(p))$
, and let
$S_2(\Gamma _0(p))$
, and let
![]() $F=f_1\otimes f_2\otimes f_3$
. We work under the following assumption on the sign of the functional equation (3.1).
$F=f_1\otimes f_2\otimes f_3$
. We work under the following assumption on the sign of the functional equation (3.1).
Assumption 4.1
![]() $W(F)=+1. $
$W(F)=+1. $
Under Assumption 4.1, the L-function
![]() $L(F, s)$
vanishes to even order at the central critical point
$L(F, s)$
vanishes to even order at the central critical point
![]() $s=2$
, by (3.3), and the Beilinson–Bloch conjecture (3.5) predicts that the algebraic rank of the F-isotypic component of
$s=2$
, by (3.3), and the Beilinson–Bloch conjecture (3.5) predicts that the algebraic rank of the F-isotypic component of
![]() $\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})$
is even. Comparing with the situation of Heegner points on modular curves studied in [Reference Gross and Zagier13], it seems reasonable to expect that the F-isotypic component of
$\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})$
is even. Comparing with the situation of Heegner points on modular curves studied in [Reference Gross and Zagier13], it seems reasonable to expect that the F-isotypic component of
![]() $\Delta _{\operatorname {\mathrm {GKS}}}(e)$
is trivial, for all
$\Delta _{\operatorname {\mathrm {GKS}}}(e)$
is trivial, for all
![]() $e\in X(\mathbb {Q})$
. While this appears to be difficult to show directly in the Chow group, we can prove the corresponding statement for the image of the cycle under the complex Abel–Jacobi map
$e\in X(\mathbb {Q})$
. While this appears to be difficult to show directly in the Chow group, we can prove the corresponding statement for the image of the cycle under the complex Abel–Jacobi map
 $$ \begin{align} \operatorname{\mathrm{AJ}}_{X^3} : \operatorname{\mathrm{CH}}^2(X_{\mathbb{C}}^3)_0(\mathbb{C}){\longrightarrow} J^2(X^3_{\mathbb{C}}) :=\frac{(\operatorname{\mathrm{Fil}}^{2} H^{3}_{\operatorname{\mathrm{dR}}}(X_{\mathbb{C}}^3))^\vee}{\operatorname{\mathrm{Im}} H_{3}(X^3_{\mathbb{C}}(\mathbb{C}), \mathbb{Z})}, \end{align} $$
$$ \begin{align} \operatorname{\mathrm{AJ}}_{X^3} : \operatorname{\mathrm{CH}}^2(X_{\mathbb{C}}^3)_0(\mathbb{C}){\longrightarrow} J^2(X^3_{\mathbb{C}}) :=\frac{(\operatorname{\mathrm{Fil}}^{2} H^{3}_{\operatorname{\mathrm{dR}}}(X_{\mathbb{C}}^3))^\vee}{\operatorname{\mathrm{Im}} H_{3}(X^3_{\mathbb{C}}(\mathbb{C}), \mathbb{Z})}, \end{align} $$
whose target is the second Griffiths intermediate Jacobian of
![]() $X^3_{\mathbb {C}}$
. This map is a higher dimensional generalization of the familiar Abel–Jacobi isomorphism for curves. It is defined by the integration formula
$X^3_{\mathbb {C}}$
. This map is a higher dimensional generalization of the familiar Abel–Jacobi isomorphism for curves. It is defined by the integration formula
 $$\begin{align*}\operatorname{\mathrm{AJ}}_{X^3}(Z)(\alpha):=\int_{\partial^{-1}(Z)} \alpha, \quad \text{for all } \alpha\in \operatorname{\mathrm{Fil}}^{2} H^{3}_{\operatorname{\mathrm{dR}}}(X^3_{\mathbb{C}}), \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{AJ}}_{X^3}(Z)(\alpha):=\int_{\partial^{-1}(Z)} \alpha, \quad \text{for all } \alpha\in \operatorname{\mathrm{Fil}}^{2} H^{3}_{\operatorname{\mathrm{dR}}}(X^3_{\mathbb{C}}), \end{align*}$$
where
![]() $\partial ^{-1}(Z)$
denotes any continuous
$\partial ^{-1}(Z)$
denotes any continuous
![]() $3$
-chain in
$3$
-chain in
![]() $X^3_{\mathbb {C}}(\mathbb {C})$
whose image under the boundary map
$X^3_{\mathbb {C}}(\mathbb {C})$
whose image under the boundary map
![]() $\partial $
is Z.
$\partial $
is Z.
Definition 4.1 Given a point e in
![]() $X(\bar {\mathbb {Q}})$
and a choice of correspondence
$X(\bar {\mathbb {Q}})$
and a choice of correspondence
![]() $t_F$
(3.4) projecting to the F-isotypic component of
$t_F$
(3.4) projecting to the F-isotypic component of
![]() $H^0(X^3, \Omega ^3_{X^3})\otimes \mathbb {R}$
, define the F-isotypic component of the Abel–Jacobi image of the Gross–Kudla–Schoen cycle by
$H^0(X^3, \Omega ^3_{X^3})\otimes \mathbb {R}$
, define the F-isotypic component of the Abel–Jacobi image of the Gross–Kudla–Schoen cycle by
Remark 4.2 Definition 4.1 is independent of the choice of
![]() $t_F$
, as
$t_F$
, as
![]() $\operatorname {\mathrm {AJ}}_{X^3}$
is functorial and any two such projectors act similarly on cohomology.
$\operatorname {\mathrm {AJ}}_{X^3}$
is functorial and any two such projectors act similarly on cohomology.
Henceforth, we fix a choice of projector
![]() $t_F=t_{f_1}\otimes t_{f_2}\otimes t_{f_3}$
. The aim of this section is to prove the main result:
$t_F=t_{f_1}\otimes t_{f_2}\otimes t_{f_3}$
. The aim of this section is to prove the main result:
Theorem 4.3 Let
![]() $f_1, f_2$
, and
$f_1, f_2$
, and
![]() $f_3$
be three normalized eigenforms in
$f_3$
be three normalized eigenforms in
![]() $S_2(\Gamma _0(p))$
, denote by
$S_2(\Gamma _0(p))$
, denote by
![]() $F=f_1\otimes f_2\otimes f_3$
their triple product, and suppose that F satisfies Assumption 4.1. Then
$F=f_1\otimes f_2\otimes f_3$
their triple product, and suppose that F satisfies Assumption 4.1. Then
![]() $\operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(e))=0$
in
$\operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(e))=0$
in
![]() $J^2(X^3_{\mathbb {C}})_{K_F}$
, for all
$J^2(X^3_{\mathbb {C}})_{K_F}$
, for all
![]() $e\in X(\mathbb {Q})$
.
$e\in X(\mathbb {Q})$
.
Remark 4.4 Similar arguments to the ones presented in the proof of Theorem 4.3 below can be used to prove that the image of
![]() $(t_F)_*(\Delta _{\operatorname {\mathrm {GKS}}}(e))$
under Bloch’s [Reference Bloch4]
$(t_F)_*(\Delta _{\operatorname {\mathrm {GKS}}}(e))$
under Bloch’s [Reference Bloch4]
![]() $\ell $
-adic étale Abel–Jacobi map
$\ell $
-adic étale Abel–Jacobi map
 $$ \begin{align} \operatorname{\mathrm{AJ}}^{\operatorname{\mathrm{et}}}_{X^3} : \operatorname{\mathrm{CH}}^2(X^3)_0(\mathbb{Q}) {\longrightarrow} H^1(\mathbb{Q}, H^{3}_{\operatorname{\mathrm{et}}}(X^3_{\bar{\mathbb{Q}}}, \mathbb{Q}_\ell(2))) \end{align} $$
$$ \begin{align} \operatorname{\mathrm{AJ}}^{\operatorname{\mathrm{et}}}_{X^3} : \operatorname{\mathrm{CH}}^2(X^3)_0(\mathbb{Q}) {\longrightarrow} H^1(\mathbb{Q}, H^{3}_{\operatorname{\mathrm{et}}}(X^3_{\bar{\mathbb{Q}}}, \mathbb{Q}_\ell(2))) \end{align} $$
is torsion, when the global root number is
![]() $W(F)=+1$
. It is conjectured that for any smooth proper variety over a number field, and for any prime
$W(F)=+1$
. It is conjectured that for any smooth proper variety over a number field, and for any prime
![]() $\ell $
, the
$\ell $
, the
![]() $\ell $
-adic Abel–Jacobi maps in any codimension are injective up to torsion [Reference Jannsen16, Conjecture 9.15]. Thus, conditional on this conjecture,
$\ell $
-adic Abel–Jacobi maps in any codimension are injective up to torsion [Reference Jannsen16, Conjecture 9.15]. Thus, conditional on this conjecture,
![]() $(t_F)_*(\Delta _{\operatorname {\mathrm {GKS}}}(e))$
is trivial in the Chow group
$(t_F)_*(\Delta _{\operatorname {\mathrm {GKS}}}(e))$
is trivial in the Chow group
![]() $\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})_{K_F}$
.
$\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})_{K_F}$
.
The rest of this section constitutes the proof of Theorem 4.3. We distinguish different situations depending on the genus
![]() $g_X$
of X, which we recall is given by the formula (2.2). The curve X has genus zero exactly when
$g_X$
of X, which we recall is given by the formula (2.2). The curve X has genus zero exactly when
![]() $p\in \{ 2, 3, 5, 7, 13\}$
. In this case, the space of cusp forms
$p\in \{ 2, 3, 5, 7, 13\}$
. In this case, the space of cusp forms
![]() $S_2(\Gamma _0(p))$
is trivial, and there is no triple product L-function to consider in the first place. We have
$S_2(\Gamma _0(p))$
is trivial, and there is no triple product L-function to consider in the first place. We have
![]() $\Delta _{\operatorname {\mathrm {GKS}}}(e)=0$
in
$\Delta _{\operatorname {\mathrm {GKS}}}(e)=0$
in
![]() $\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})$
, as the cycle class map is injective in this case [Reference Gross and Schoen12, Proposition 4.1].
$\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})$
, as the cycle class map is injective in this case [Reference Gross and Schoen12, Proposition 4.1].
4.1 The genus one case
Suppose that
![]() $g_X=1$
, i.e.,
$g_X=1$
, i.e.,
![]() $p\in \{ 11, 17, 19\}$
. In this case, X is an elliptic curve over
$p\in \{ 11, 17, 19\}$
. In this case, X is an elliptic curve over
![]() $\mathbb {Q}$
of Mordell–Weil rank
$\mathbb {Q}$
of Mordell–Weil rank
![]() $0$
. For all
$0$
. For all
![]() $e\in X(\mathbb {Q})$
, we have
$e\in X(\mathbb {Q})$
, we have
![]() $6\Delta _{\operatorname {\mathrm {GKS}}}(e)=0$
in
$6\Delta _{\operatorname {\mathrm {GKS}}}(e)=0$
in
![]() $\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})$
[Reference Gross and Schoen12, Corollary 4.7]. On the L-function side,
$\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})$
[Reference Gross and Schoen12, Corollary 4.7]. On the L-function side,
![]() $f_1=f_2=f_3=f$
is the normalized eigenform corresponding to the elliptic curve X. By [Reference Gross and Kudla11,
$f_1=f_2=f_3=f$
is the normalized eigenform corresponding to the elliptic curve X. By [Reference Gross and Kudla11,
![]() $(11.8)$
] the triple product L-function decomposes as
$(11.8)$
] the triple product L-function decomposes as
Note that
![]() $W(F)=a_p(f)^3=a_p(f)=W(f)=+1$
by (3.2) and the fact that the sign of the functional equation of
$W(F)=a_p(f)^3=a_p(f)=W(f)=+1$
by (3.2) and the fact that the sign of the functional equation of
![]() $L(f, s)$
centered at
$L(f, s)$
centered at
![]() $s=1$
is equal to
$s=1$
is equal to
![]() $+1$
, since X has Mordell–Weil rank
$+1$
, since X has Mordell–Weil rank
![]() $0$
. For each
$0$
. For each
![]() $p\in \{ 11, 17, 19\}$
, we have
$p\in \{ 11, 17, 19\}$
, we have
![]() $L(F, 2)\neq 0$
[Reference Gross and Kudla11, Tables 12.5–12.7]. In other words,
$L(F, 2)\neq 0$
[Reference Gross and Kudla11, Tables 12.5–12.7]. In other words,
![]() $\operatorname {\mathrm {ord}}_{s=2}(L(F, s))=0$
. The fact that
$\operatorname {\mathrm {ord}}_{s=2}(L(F, s))=0$
. The fact that
![]() $\Delta _{\operatorname {\mathrm {GKS}}}(e)$
is torsion in the Chow group is therefore consistent with the Beilinson–Bloch conjecture (3.5).
$\Delta _{\operatorname {\mathrm {GKS}}}(e)$
is torsion in the Chow group is therefore consistent with the Beilinson–Bloch conjecture (3.5).
4.2 The higher genus case
Suppose that
![]() $g_X\geq 2$
. It will be convenient to sometimes view the Atkin–Lehner involution
$g_X\geq 2$
. It will be convenient to sometimes view the Atkin–Lehner involution
![]() $w_p$
of Section 2.1 as a correspondence by taking its graph. By slight abuse of notation, we will write
$w_p$
of Section 2.1 as a correspondence by taking its graph. By slight abuse of notation, we will write
 $w_p \in \mathrm {Corr}^0(X, X)(\mathbb {Q})$
. The operator
$w_p \in \mathrm {Corr}^0(X, X)(\mathbb {Q})$
. The operator
![]() $w_p$
naturally belongs to the Hecke algebra
$w_p$
naturally belongs to the Hecke algebra
![]() $\mathbb {T}$
by (2.5), and commutes with the Hecke operators. The modular forms
$\mathbb {T}$
by (2.5), and commutes with the Hecke operators. The modular forms
![]() $f_j$
, with
$f_j$
, with
![]() $j\in \{1, 2, 3\}$
, are eigenforms for the operator
$j\in \{1, 2, 3\}$
, are eigenforms for the operator
![]() $w_p$
with eigenvalues given by
$w_p$
with eigenvalues given by
![]() $-a_p(f_j)$
respectively (see Section 2.1).
$-a_p(f_j)$
respectively (see Section 2.1).
Consider the involution
![]() $u_p:=w_p\times w_p\times w_p$
of
$u_p:=w_p\times w_p\times w_p$
of
![]() $X^3$
. By taking its graph, it may be viewed as a correspondence, and we write again
$X^3$
. By taking its graph, it may be viewed as a correspondence, and we write again
 $u_p\in \mathrm {Corr}^0(X^3, X^3)(\mathbb {Q})$
, by slight abuse of notation. Note that, as correspondences, we have
$u_p\in \mathrm {Corr}^0(X^3, X^3)(\mathbb {Q})$
, by slight abuse of notation. Note that, as correspondences, we have
 $$\begin{align*}u_p = w_p\otimes w_p \otimes w_p :=\operatorname{\mathrm{pr}}_{14}^*(w_p)\cdot \operatorname{\mathrm{pr}}_{25}^*(w_p)\cdot \operatorname{\mathrm{pr}}_{36}^*(w_p) \in \mathrm{Corr}^{0}(X^3, X^3)(\mathbb{Q}). \end{align*}$$
$$\begin{align*}u_p = w_p\otimes w_p \otimes w_p :=\operatorname{\mathrm{pr}}_{14}^*(w_p)\cdot \operatorname{\mathrm{pr}}_{25}^*(w_p)\cdot \operatorname{\mathrm{pr}}_{36}^*(w_p) \in \mathrm{Corr}^{0}(X^3, X^3)(\mathbb{Q}). \end{align*}$$
The map
![]() $u_p$
induces an involution on cohomology via pull-back, hence an involution on the space of cusp forms of weight
$u_p$
induces an involution on cohomology via pull-back, hence an involution on the space of cusp forms of weight
![]() $(2, 2, 2)$
for
$(2, 2, 2)$
for
![]() $\Gamma _0(p)^3$
. By (3.2), we see that
$\Gamma _0(p)^3$
. By (3.2), we see that
 $$ \begin{align} u_p^*(F)=-W(F)\cdot F. \end{align} $$
$$ \begin{align} u_p^*(F)=-W(F)\cdot F. \end{align} $$
Lemma 4.5 We have
![]() $ (u_p)_*(\Delta _{\operatorname {\mathrm {GKS}}}(e))=\Delta _{\operatorname {\mathrm {GKS}}}(w_p(e)), $
for any
$ (u_p)_*(\Delta _{\operatorname {\mathrm {GKS}}}(e))=\Delta _{\operatorname {\mathrm {GKS}}}(w_p(e)), $
for any
![]() $e\in X(\bar {\mathbb {Q}})$
.
$e\in X(\bar {\mathbb {Q}})$
.
Proof The induced map
 $(u_p)_* : \operatorname {\mathrm {CH}}^2(X^3) {\longrightarrow } \operatorname {\mathrm {CH}}^2(X^3)$
on Chow groups simply maps a cycle to its image under
$(u_p)_* : \operatorname {\mathrm {CH}}^2(X^3) {\longrightarrow } \operatorname {\mathrm {CH}}^2(X^3)$
on Chow groups simply maps a cycle to its image under
![]() $u_p$
. We have
$u_p$
. We have
![]() $u_p(\Delta )=\Delta $
, since
$u_p(\Delta )=\Delta $
, since
![]() $u_p$
is an automorphism of
$u_p$
is an automorphism of
![]() $X^3$
. However,
$X^3$
. However,
![]() $u_p(P_T(e)_*(\Delta ))=P_T(w_p(e))_*(\Delta )$
for any proper subset
$u_p(P_T(e)_*(\Delta ))=P_T(w_p(e))_*(\Delta )$
for any proper subset
![]() $T \text{ of } \{ 1,2,3\}$
.▪
$T \text{ of } \{ 1,2,3\}$
.▪
Proposition 4.6 Let
![]() $f_1, f_2$
, and
$f_1, f_2$
, and
![]() $f_3$
be three normalized eigenforms in
$f_3$
be three normalized eigenforms in
![]() $S_2(\Gamma _0(p))$
, denote by
$S_2(\Gamma _0(p))$
, denote by
![]() $F=f_1\otimes f_2\otimes f_3$
their triple product, and suppose that F satisfies Assumption 4.1. For any point
$F=f_1\otimes f_2\otimes f_3$
their triple product, and suppose that F satisfies Assumption 4.1. For any point
![]() $e\in X(\bar {\mathbb {Q}})$
, we have
$e\in X(\bar {\mathbb {Q}})$
, we have
 $ \operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(e))=-\operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(w_p(e))). $
$ \operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(e))=-\operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(w_p(e))). $
Proof By functoriality of Abel–Jacobi maps with respect to correspondences, we have
 $$ \begin{align} \operatorname{\mathrm{AJ}}_{X^3}((u_p)_*(t_F)_*(\Delta_{\operatorname{\mathrm{GKS}}}(e)))=(u_p^*)^\vee \operatorname{\mathrm{AJ}}_{X^3}^F(\Delta_{\operatorname{\mathrm{GKS}}}(e)). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{AJ}}_{X^3}((u_p)_*(t_F)_*(\Delta_{\operatorname{\mathrm{GKS}}}(e)))=(u_p^*)^\vee \operatorname{\mathrm{AJ}}_{X^3}^F(\Delta_{\operatorname{\mathrm{GKS}}}(e)). \end{align} $$
For
![]() $i\in \{1, 2, 3\}$
,
$i\in \{1, 2, 3\}$
,
![]() $w_p$
commutes with
$w_p$
commutes with
![]() $t_{f_i}$
as self-correspondences of X up to vertical and horizontal divisors, by (2.5) and (2.6). This implies that
$t_{f_i}$
as self-correspondences of X up to vertical and horizontal divisors, by (2.5) and (2.6). This implies that
 $$ \begin{align*} u_p \circ t_F &= (w_p \circ t_{f_1}) \otimes (w_p \circ t_{f_2}) \otimes (w_p \circ t_{f_3}) \\ &= (t^{\prime}_{f_1}\circ w_p) \otimes (t^{\prime}_{f_2}\circ w_p) \otimes (t^{\prime}_{f_3}\circ w_p) = t^{\prime}_F\circ u_p, \end{align*} $$
$$ \begin{align*} u_p \circ t_F &= (w_p \circ t_{f_1}) \otimes (w_p \circ t_{f_2}) \otimes (w_p \circ t_{f_3}) \\ &= (t^{\prime}_{f_1}\circ w_p) \otimes (t^{\prime}_{f_2}\circ w_p) \otimes (t^{\prime}_{f_3}\circ w_p) = t^{\prime}_F\circ u_p, \end{align*} $$
where
 $t^{\prime }_F=t^{\prime }_{f_1}\otimes t^{\prime }_{f_2}\otimes t^{\prime }_{f_3}$
is possibly another F-isotypic projector. In particular, using Lemma 4.5, we obtain
$t^{\prime }_F=t^{\prime }_{f_1}\otimes t^{\prime }_{f_2}\otimes t^{\prime }_{f_3}$
is possibly another F-isotypic projector. In particular, using Lemma 4.5, we obtain
The left hand side of (4.4) is thus equal to
 $\operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(w_p(e)))$
by Remark 4.2.
$\operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(w_p(e)))$
by Remark 4.2.
On the other hand,
![]() $\operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(e))$
lies in
$\operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(e))$
lies in
![]() $(t_F^*)^\vee (J^2(X^3_{\mathbb {C}}))$
by functoriality of the complex Abel–Jacobi map with respect to correspondences, that is, in the F-isotypic Hecke component of the intermediate Jacobian. The triple product Hecke algebra
$(t_F^*)^\vee (J^2(X^3_{\mathbb {C}}))$
by functoriality of the complex Abel–Jacobi map with respect to correspondences, that is, in the F-isotypic Hecke component of the intermediate Jacobian. The triple product Hecke algebra
![]() $\mathbb {T}^{\otimes 3}$
acts via correspondences on the latter by multiplication by the Hecke eigenvalues of F. For any
$\mathbb {T}^{\otimes 3}$
acts via correspondences on the latter by multiplication by the Hecke eigenvalues of F. For any
 $\alpha \in \operatorname {\mathrm {Fil}}^{2} H^{3}_{\operatorname {\mathrm {dR}}}(X^3_{\mathbb {C}})$
, we have the equality
$\alpha \in \operatorname {\mathrm {Fil}}^{2} H^{3}_{\operatorname {\mathrm {dR}}}(X^3_{\mathbb {C}})$
, we have the equality
 $$\begin{align*}(u_p^*)^\vee \operatorname{\mathrm{AJ}}_{X^3}^F(\Delta_{\operatorname{\mathrm{GKS}}}(e))(\alpha)=\operatorname{\mathrm{AJ}}_{X^3}(\Delta_{\operatorname{\mathrm{GKS}}}(e))(u_p^*(t_F^*(\alpha))). \end{align*}$$
$$\begin{align*}(u_p^*)^\vee \operatorname{\mathrm{AJ}}_{X^3}^F(\Delta_{\operatorname{\mathrm{GKS}}}(e))(\alpha)=\operatorname{\mathrm{AJ}}_{X^3}(\Delta_{\operatorname{\mathrm{GKS}}}(e))(u_p^*(t_F^*(\alpha))). \end{align*}$$
The operator
![]() $u_p$
in
$u_p$
in
![]() $ \mathbb {T}^{\otimes 3}$
acts via pull-back on the F-isotypic component
$ \mathbb {T}^{\otimes 3}$
acts via pull-back on the F-isotypic component
![]() $(t_F)^*H_{\operatorname {\mathrm {dR}}}^3(X^3_{\mathbb {C}})$
as multiplication by
$(t_F)^*H_{\operatorname {\mathrm {dR}}}^3(X^3_{\mathbb {C}})$
as multiplication by
![]() $-W(F)$
by (4.3). In particular,
$-W(F)$
by (4.3). In particular,
 $u_p^*(t_F^*(\alpha ))=-W(F) t_F^*(\alpha )$
. By Assumption 4.1, the right hand side of (4.4) is thus
$u_p^*(t_F^*(\alpha ))=-W(F) t_F^*(\alpha )$
. By Assumption 4.1, the right hand side of (4.4) is thus
![]() $- \operatorname {\mathrm {AJ}}_{X^3}^F (\Delta _{\operatorname {\mathrm {GKS}}}(e)).$
▪
$- \operatorname {\mathrm {AJ}}_{X^3}^F (\Delta _{\operatorname {\mathrm {GKS}}}(e)).$
▪
Mazur proved, for
![]() $g_X\geq 2$
and
$g_X\geq 2$
and
![]() $p\not \in \{ 37, 43, 67, 163\}$
, that
$p\not \in \{ 37, 43, 67, 163\}$
, that
![]() $X(\mathbb {Q})=\{ \xi _\infty , \xi _0 \},$
where we recall that
$X(\mathbb {Q})=\{ \xi _\infty , \xi _0 \},$
where we recall that
![]() $\xi _\infty $
and
$\xi _\infty $
and
![]() $\xi _0$
denote the two cusps of X [Reference Mazur22, Theorem 1]. Moreover, the modular curve
$\xi _0$
denote the two cusps of X [Reference Mazur22, Theorem 1]. Moreover, the modular curve
![]() $X_0(37)$
has two noncuspidal
$X_0(37)$
has two noncuspidal
![]() $\mathbb {Q}$
-rational points, while
$\mathbb {Q}$
-rational points, while
![]() $X_0(p)$
has a unique noncuspidal
$X_0(p)$
has a unique noncuspidal
![]() $\mathbb {Q}$
-rational point, for
$\mathbb {Q}$
-rational point, for
![]() $p\in \{ 43, 67, 163\}$
.
$p\in \{ 43, 67, 163\}$
.
Corollary 4.7 Let
![]() $f_1, f_2$
, and
$f_1, f_2$
, and
![]() $f_3$
be three normalized eigenforms in
$f_3$
be three normalized eigenforms in
![]() $S_2(\Gamma _0(p))$
, denote by
$S_2(\Gamma _0(p))$
, denote by
![]() $F=f_1\otimes f_2\otimes f_3$
their triple product, and suppose that F satisfies Assumption
4.1
. If p belongs to
$F=f_1\otimes f_2\otimes f_3$
their triple product, and suppose that F satisfies Assumption
4.1
. If p belongs to
![]() $\{ 43, 67, 163 \}$
, and e denotes the unique noncuspidal
$\{ 43, 67, 163 \}$
, and e denotes the unique noncuspidal
![]() $\mathbb {Q}$
-rational point of X, then
$\mathbb {Q}$
-rational point of X, then
![]() $ \operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(e))=0$
.
$ \operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(e))=0$
.
Proof The involution
![]() $w_p$
maps
$w_p$
maps
![]() $\mathbb {Q}$
-rational points to
$\mathbb {Q}$
-rational points to
![]() $\mathbb {Q}$
-rational points and permutes the two cusps
$\mathbb {Q}$
-rational points and permutes the two cusps
![]() $\xi _\infty $
to
$\xi _\infty $
to
![]() $\xi _0$
. It therefore fixes the noncuspidal point e, and the result follows from Proposition 4.6.▪
$\xi _0$
. It therefore fixes the noncuspidal point e, and the result follows from Proposition 4.6.▪
Corollary 4.8 Let
![]() $f_1, f_2$
, and
$f_1, f_2$
, and
![]() $f_3$
be three normalized eigenforms in
$f_3$
be three normalized eigenforms in
![]() $S_2(\Gamma _0(p))$
, denote by
$S_2(\Gamma _0(p))$
, denote by
![]() $F=f_1\otimes f_2\otimes f_3$
their triple product, and suppose that F satisfies Assumption 4.1. If
$F=f_1\otimes f_2\otimes f_3$
their triple product, and suppose that F satisfies Assumption 4.1. If
![]() $g_X\geq 2$
, then
$g_X\geq 2$
, then
![]() $ \operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty ))=\operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _0))=0. $
$ \operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty ))=\operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _0))=0. $
Proof Gross and Schoen [Reference Gross and Schoen12, Proposition 3.6] have constructed a correspondence
![]() $\Xi $
in
$\Xi $
in
![]() $\mathrm {Corr}^{1}(X, X^3)(\mathbb {Q})$
with the property that the natural transformation induced by push-forward
$\mathrm {Corr}^{1}(X, X^3)(\mathbb {Q})$
with the property that the natural transformation induced by push-forward
sends the rational equivalence class of a divisor
![]() $\sum m(e)e$
to
$\sum m(e)e$
to
![]() $\sum m(e)\Delta _{\operatorname {\mathrm {GKS}}}(e)$
. In particular, the cycle
$\sum m(e)\Delta _{\operatorname {\mathrm {GKS}}}(e)$
. In particular, the cycle
![]() $\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty )-\Delta _{\operatorname {\mathrm {GKS}}}(\xi _0)$
in
$\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty )-\Delta _{\operatorname {\mathrm {GKS}}}(\xi _0)$
in
![]() $\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})$
depends only on the class of the degree zero divisor
$\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q})$
depends only on the class of the degree zero divisor
![]() $(\xi _\infty )-(\xi _0)$
in
$(\xi _\infty )-(\xi _0)$
in
![]() $\operatorname {\mathrm {CH}}^1(X)_0(\mathbb {Q})=J(\mathbb {Q})$
. By Manin–Drinfeld [Reference Manin20], the divisor
$\operatorname {\mathrm {CH}}^1(X)_0(\mathbb {Q})=J(\mathbb {Q})$
. By Manin–Drinfeld [Reference Manin20], the divisor
![]() $(\xi _\infty )-(\xi _0)$
is torsion in the Jacobian J. It follows that
$(\xi _\infty )-(\xi _0)$
is torsion in the Jacobian J. It follows that
![]() $ \Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty )-\Delta _{\operatorname {\mathrm {GKS}}}(\xi _0) $
is torsion in
$ \Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty )-\Delta _{\operatorname {\mathrm {GKS}}}(\xi _0) $
is torsion in
![]() $\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q}),$
and in particular
$\operatorname {\mathrm {CH}}^2(X^3)_0(\mathbb {Q}),$
and in particular
![]() $ \operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty ))-\operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _0))=0 $
in
$ \operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty ))-\operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _0))=0 $
in
![]() $J^{2}(X^3_{\mathbb {C}})_{K_F}$
. The involution
$J^{2}(X^3_{\mathbb {C}})_{K_F}$
. The involution
![]() $w_p$
permutes the cusps
$w_p$
permutes the cusps
![]() $\xi _\infty $
and
$\xi _\infty $
and
![]() $\xi _0$
. By Proposition 4.6, we thus have the equality
$\xi _0$
. By Proposition 4.6, we thus have the equality
![]() $ \operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty ))=-\operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _0)), $
and the proof is complete.▪
$ \operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty ))=-\operatorname {\mathrm {AJ}}_{X^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _0)), $
and the proof is complete.▪
4.3 The case
 $p=37$
$p=37$
To complete the proof of Theorem 4.3, the only remaining case is the one where
![]() $p=37$
and the chosen base point is a noncuspidal
$p=37$
and the chosen base point is a noncuspidal
![]() $\mathbb {Q}$
-rational point. The curve
$\mathbb {Q}$
-rational point. The curve
![]() $X_0(37)$
has been extensively studied by Mazur and Swinnerton-Dyer [Reference Mazur and Swinnerton-Dyer23, Section 5]. It has genus
$X_0(37)$
has been extensively studied by Mazur and Swinnerton-Dyer [Reference Mazur and Swinnerton-Dyer23, Section 5]. It has genus
![]() $2$
and is therefore hyperelliptic. Its hyperelliptic involution will be denoted by S. In particular, for all points e in
$2$
and is therefore hyperelliptic. Its hyperelliptic involution will be denoted by S. In particular, for all points e in
![]() $X_0(37)(\bar {\mathbb {Q}})$
, we have
$X_0(37)(\bar {\mathbb {Q}})$
, we have
![]() $6\Delta _{\operatorname {\mathrm {GKS}}}(e)=0$
in the Griffiths group
$6\Delta _{\operatorname {\mathrm {GKS}}}(e)=0$
in the Griffiths group
![]() $\operatorname {\mathrm {Gr}}^2(X_0(37)^3)$
of null-homologous algebraic cycles modulo algebraic equivalence [Reference Gross and Schoen12, Corollary 4.9]. The involution S is distinct from the Atkin–Lehner involution
$\operatorname {\mathrm {Gr}}^2(X_0(37)^3)$
of null-homologous algebraic cycles modulo algebraic equivalence [Reference Gross and Schoen12, Corollary 4.9]. The involution S is distinct from the Atkin–Lehner involution
![]() $w_{37}$
, as the quotient
$w_{37}$
, as the quotient
![]() $X_0(37)/w_{37}$
has genus
$X_0(37)/w_{37}$
has genus
![]() $1$
. Since S commutes with every automorphism of
$1$
. Since S commutes with every automorphism of
![]() $X_0(37)$
[Reference Mazur and Swinnerton-Dyer23, p. 27], it commutes in particular with
$X_0(37)$
[Reference Mazur and Swinnerton-Dyer23, p. 27], it commutes in particular with
![]() $w_{37}$
, and we can define another involution
$w_{37}$
, and we can define another involution
![]() $T=S\circ w_{37}=w_{37}\circ S$
. Let
$T=S\circ w_{37}=w_{37}\circ S$
. Let
![]() $\gamma _0=T(\xi _0)$
and
$\gamma _0=T(\xi _0)$
and
![]() $\gamma _\infty =T(\xi _\infty )$
be the images of the two cusps by T. By [Reference Mazur and Swinnerton-Dyer23, Proposition 2], we have
$\gamma _\infty =T(\xi _\infty )$
be the images of the two cusps by T. By [Reference Mazur and Swinnerton-Dyer23, Proposition 2], we have
We now complete the proof of Theorem 4.3.
Corollary 4.9 Let
![]() $f_1, f_2$
, and
$f_1, f_2$
, and
![]() $f_3$
be three normalized eigenforms in
$f_3$
be three normalized eigenforms in
![]() $S_2(\Gamma _0(37))$
, denote by
$S_2(\Gamma _0(37))$
, denote by
![]() $F=f_1\otimes f_2\otimes f_3$
their triple product, and suppose that F satisfies Assumption
4.1
. Then
$F=f_1\otimes f_2\otimes f_3$
their triple product, and suppose that F satisfies Assumption
4.1
. Then
 $$ \begin{align*}\operatorname{\mathrm{AJ}}_{X_0(37)^3}^F(\Delta_{\operatorname{\mathrm{GKS}}}(\gamma_0))=\operatorname{\mathrm{AJ}}_{X_0(37)^3}^F(\Delta_{\operatorname{\mathrm{GKS}}}(\gamma_\infty))=0.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{AJ}}_{X_0(37)^3}^F(\Delta_{\operatorname{\mathrm{GKS}}}(\gamma_0))=\operatorname{\mathrm{AJ}}_{X_0(37)^3}^F(\Delta_{\operatorname{\mathrm{GKS}}}(\gamma_\infty))=0.\end{align*} $$
Proof By (4.6), the Atkin–Lehner involution
![]() $w_{37}$
interchanges
$w_{37}$
interchanges
![]() $\gamma _0$
and
$\gamma _0$
and
![]() $\gamma _\infty $
. By Proposition 4.6, we have
$\gamma _\infty $
. By Proposition 4.6, we have
 $\operatorname {\mathrm {AJ}}_{X_0(37)^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\gamma _0))=-\operatorname {\mathrm {AJ}}_{X_0(37)^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\gamma _\infty ))$
. The element
$\operatorname {\mathrm {AJ}}_{X_0(37)^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\gamma _0))=-\operatorname {\mathrm {AJ}}_{X_0(37)^3}^F(\Delta _{\operatorname {\mathrm {GKS}}}(\gamma _\infty ))$
. The element
 $$\begin{align*}2\operatorname{\mathrm{AJ}}_{X_0(37)^3}^F(\Delta_{\operatorname{\mathrm{GKS}}}(\gamma_0))=\operatorname{\mathrm{AJ}}_{X_0(37)^3}((t_F)_*(\Delta_{\operatorname{\mathrm{GKS}}}(\gamma_0)-\Delta_{\operatorname{\mathrm{GKS}}}(\gamma_\infty))) \end{align*}$$
$$\begin{align*}2\operatorname{\mathrm{AJ}}_{X_0(37)^3}^F(\Delta_{\operatorname{\mathrm{GKS}}}(\gamma_0))=\operatorname{\mathrm{AJ}}_{X_0(37)^3}((t_F)_*(\Delta_{\operatorname{\mathrm{GKS}}}(\gamma_0)-\Delta_{\operatorname{\mathrm{GKS}}}(\gamma_\infty))) \end{align*}$$
in
![]() $J^2(X_0(37)^3_{\mathbb {C}})_{K_F}$
depends only on the class of
$J^2(X_0(37)^3_{\mathbb {C}})_{K_F}$
depends only on the class of
![]() $(\gamma _0)-(\gamma _\infty )$
in
$(\gamma _0)-(\gamma _\infty )$
in
![]() $J_0(37)(\mathbb {Q})$
by the existence of (4.5). But this class is the image of the class of
$J_0(37)(\mathbb {Q})$
by the existence of (4.5). But this class is the image of the class of
![]() $(\xi _0)-(\xi _\infty )$
by the involution of
$(\xi _0)-(\xi _\infty )$
by the involution of
![]() $J_0(37)$
obtained from T by push-forward. The latter class is torsion by the Manin–Drinfeld theorem [Reference Manin20].▪
$J_0(37)$
obtained from T by push-forward. The latter class is torsion by the Manin–Drinfeld theorem [Reference Manin20].▪
5 Chow–Heegner points
Let f be a normalized eigenform in
![]() $S_2(\Gamma _0(p))$
with rational coefficients, and let
$S_2(\Gamma _0(p))$
with rational coefficients, and let
![]() $E_f$
be the optimal elliptic curve quotient of J associated with f by the Eichler–Shimura construction [Reference Shimura27]. Following Section 2.2, denote by
$E_f$
be the optimal elliptic curve quotient of J associated with f by the Eichler–Shimura construction [Reference Shimura27]. Following Section 2.2, denote by
![]() $\pi _f : J {\longrightarrow } E_f$
the natural quotient map with connected kernel. It is induced by the element
$\pi _f : J {\longrightarrow } E_f$
the natural quotient map with connected kernel. It is induced by the element
 $$\begin{align*}[m_ft_f]\in \operatorname{\mathrm{CH}}^1(X^2)(\mathbb{Q})/(\operatorname{\mathrm{pr}}_1^*\operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})+\operatorname{\mathrm{pr}}_2^*\operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})), \end{align*}$$
$$\begin{align*}[m_ft_f]\in \operatorname{\mathrm{CH}}^1(X^2)(\mathbb{Q})/(\operatorname{\mathrm{pr}}_1^*\operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})+\operatorname{\mathrm{pr}}_2^*\operatorname{\mathrm{CH}}^1(X)(\mathbb{Q})), \end{align*}$$
where
![]() $m_f\in \mathbb {N}$
denotes the denominator of
$m_f\in \mathbb {N}$
denotes the denominator of
![]() $\operatorname {\mathrm {pr}}_f\in \mathbb {T}$
.
$\operatorname {\mathrm {pr}}_f\in \mathbb {T}$
.
Remark 5.1 To the best of the author’s knowledge, it is unknown whether there are finitely or infinitely many elliptic curves over
![]() $\mathbb {Q}$
of prime conductor. It is a result of Setzer [Reference Setzer26, Theorem 2] that, given a prime p distinct from
$\mathbb {Q}$
of prime conductor. It is a result of Setzer [Reference Setzer26, Theorem 2] that, given a prime p distinct from
![]() $2, 3$
, and
$2, 3$
, and
![]() $17$
, there is an elliptic curve of conductor p over
$17$
, there is an elliptic curve of conductor p over
![]() $\mathbb {Q}$
with a rational
$\mathbb {Q}$
with a rational
![]() $2$
-torsion point if and only if
$2$
-torsion point if and only if
![]() $p=u^2+64$
for some rational integer u. A conjecture of Hardy and Littlewood [Reference Hardy and Littlewood14, Conjecture F] implies that there are infinitely many values of u such that
$p=u^2+64$
for some rational integer u. A conjecture of Hardy and Littlewood [Reference Hardy and Littlewood14, Conjecture F] implies that there are infinitely many values of u such that
![]() $u^2+64$
is prime. Thus, conditional on this conjecture of Hardy and Littlewood, there are infinitely many primes p which occur as the conductor of an elliptic curve over
$u^2+64$
is prime. Thus, conditional on this conjecture of Hardy and Littlewood, there are infinitely many primes p which occur as the conductor of an elliptic curve over
![]() $\mathbb {Q}$
. This is explained in detail in the preprint [Reference Howe and Joshi15].
$\mathbb {Q}$
. This is explained in detail in the preprint [Reference Howe and Joshi15].
Let g be an auxiliary normalized eigenform in
![]() $S_2(\Gamma _0(p))$
. Following the notations of Section 2.2, recall that
$S_2(\Gamma _0(p))$
. Following the notations of Section 2.2, recall that
![]() $\operatorname {\mathrm {pr}}_{[g]}\in \mathbb {T}$
denotes the
$\operatorname {\mathrm {pr}}_{[g]}\in \mathbb {T}$
denotes the
![]() $[g]$
-isotypic Hecke projector. Define the
$[g]$
-isotypic Hecke projector. Define the
![]() $[g]$
-isotypic component
$[g]$
-isotypic component
 $\operatorname {\mathrm {End}}_{\mathbb {Q}}^0(J)[g]:=\operatorname {\mathrm {pr}}_{[g]}\cdot \operatorname {\mathrm {End}}_{\mathbb {Q}}^0(J)$
and let
$\operatorname {\mathrm {End}}_{\mathbb {Q}}^0(J)[g]:=\operatorname {\mathrm {pr}}_{[g]}\cdot \operatorname {\mathrm {End}}_{\mathbb {Q}}^0(J)$
and let
 $\operatorname {\mathrm {CH}}^1(X^2)[g]_{\mathbb {Q}}$
be the group of cycles mapping to
$\operatorname {\mathrm {CH}}^1(X^2)[g]_{\mathbb {Q}}$
be the group of cycles mapping to
 $\operatorname {\mathrm {End}}_{\mathbb {Q}}^0(J)[g]$
under (2.6) modulo vertical and horizontal divisors. Let
$\operatorname {\mathrm {End}}_{\mathbb {Q}}^0(J)[g]$
under (2.6) modulo vertical and horizontal divisors. Let
![]() $t_{[g]}$
be an element of
$t_{[g]}$
be an element of
 $\operatorname {\mathrm {CH}}^1(X^2)[g]_{\mathbb {Q}}$
mapping to
$\operatorname {\mathrm {CH}}^1(X^2)[g]_{\mathbb {Q}}$
mapping to
![]() $\operatorname {\mathrm {pr}}_{[g]}$
.
$\operatorname {\mathrm {pr}}_{[g]}$
.
For any correspondence
![]() $Z\in \operatorname {\mathrm {CH}}^1(X^2)(\mathbb {Q})$
, define
$Z\in \operatorname {\mathrm {CH}}^1(X^2)(\mathbb {Q})$
, define
 $$ \begin{align*}\Pi_{Z}:= \operatorname{\mathrm{pr}}_{12}^*(Z) \cdot \operatorname{\mathrm{pr}}_{34}^*(\Delta)\in \operatorname{\mathrm{CH}}^2(X^4)(\mathbb{Q}), \end{align*} $$
$$ \begin{align*}\Pi_{Z}:= \operatorname{\mathrm{pr}}_{12}^*(Z) \cdot \operatorname{\mathrm{pr}}_{34}^*(\Delta)\in \operatorname{\mathrm{CH}}^2(X^4)(\mathbb{Q}), \end{align*} $$
where
![]() $\Delta \in \operatorname {\mathrm {CH}}^1(X^2)(\mathbb {Q})$
is the diagonal cycle. It induces a push-forward map
$\Delta \in \operatorname {\mathrm {CH}}^1(X^2)(\mathbb {Q})$
is the diagonal cycle. It induces a push-forward map
for any field extension L of
![]() $\mathbb {Q}$
. For
$\mathbb {Q}$
. For
![]() $e\in X(\bar {\mathbb {Q}})$
, define the point
$e\in X(\bar {\mathbb {Q}})$
, define the point
Remark 5.2 The association of a point in J to a self-correspondence is well-defined modulo vertical and horizontal divisors [Reference Daub8, Ex. 3.1.7]. Associate to
 $Z\in \operatorname {\mathrm {CH}}^1(X^2)(\mathbb {Q})_{\mathbb {Q}}$
a point
$Z\in \operatorname {\mathrm {CH}}^1(X^2)(\mathbb {Q})_{\mathbb {Q}}$
a point
![]() $P_Z(e):=P_{mZ}(e)\otimes 1/m \in J(\bar {\mathbb {Q}})_{\mathbb {Q}}$
, where
$P_Z(e):=P_{mZ}(e)\otimes 1/m \in J(\bar {\mathbb {Q}})_{\mathbb {Q}}$
, where
![]() $m\in \mathbb {N}$
such that
$m\in \mathbb {N}$
such that
![]() $mZ\in \operatorname {\mathrm {CH}}^1(X^2)(\mathbb {Q})$
.
$mZ\in \operatorname {\mathrm {CH}}^1(X^2)(\mathbb {Q})$
.
By composing correspondences, we can define
 $$ \begin{align} \Pi_{Z,t_f}:=(m_ft_f) \circ \Pi_{Z} = \operatorname{\mathrm{pr}}_{12}^*(Z) \cdot \operatorname{\mathrm{pr}}_{34}^*(m_ft_f) \in \mathrm{Corr}^{-1}(X^3, X)(\mathbb{Q}). \end{align} $$
$$ \begin{align} \Pi_{Z,t_f}:=(m_ft_f) \circ \Pi_{Z} = \operatorname{\mathrm{pr}}_{12}^*(Z) \cdot \operatorname{\mathrm{pr}}_{34}^*(m_ft_f) \in \mathrm{Corr}^{-1}(X^3, X)(\mathbb{Q}). \end{align} $$
This induces, in the terminology of [Reference Bertolini, Darmon and Prasanna2], a generalized modular parametrization
 $$\begin{align*}\Pi_{Z}^f:=\Pi_{Z,t_f,*}= \pi_f \circ \Pi_{Z, *} : \operatorname{\mathrm{CH}}^2(X^3)_0(L) {\longrightarrow} E_f(L), \end{align*}$$
$$\begin{align*}\Pi_{Z}^f:=\Pi_{Z,t_f,*}= \pi_f \circ \Pi_{Z, *} : \operatorname{\mathrm{CH}}^2(X^3)_0(L) {\longrightarrow} E_f(L), \end{align*}$$
independent of the choice of
![]() $t_f$
. Given
$t_f$
. Given
![]() $e\in X(\bar {\mathbb {Q}})$
, we define the Chow–Heegner point
$e\in X(\bar {\mathbb {Q}})$
, we define the Chow–Heegner point
 $$\begin{align*}P_{Z}^f(e) := \Pi_Z^f(\Delta_{\operatorname{\mathrm{GKS}}}(e))=\pi_f(P_Z(e))\in E_f(\bar{\mathbb{Q}}). \end{align*}$$
$$\begin{align*}P_{Z}^f(e) := \Pi_Z^f(\Delta_{\operatorname{\mathrm{GKS}}}(e))=\pi_f(P_Z(e))\in E_f(\bar{\mathbb{Q}}). \end{align*}$$
By Remark 5.2, we can define the Chow–Heegner point associated with f and
![]() $[g]$
by
$[g]$
by
 $$\begin{align*}P_{[g]}^f(e):=P_{t_{[g]}}^f(e) \in E_f(\bar{\mathbb{Q}})_{\mathbb{Q}}. \end{align*}$$
$$\begin{align*}P_{[g]}^f(e):=P_{t_{[g]}}^f(e) \in E_f(\bar{\mathbb{Q}})_{\mathbb{Q}}. \end{align*}$$
Concretely, we have
 $$\begin{align*}P_{[g]}^f(e)=\pi_f(\Pi_{m_{[g]}t_{[g]},*}(\Delta_{\operatorname{\mathrm{GKS}}}(e)))\otimes 1/m_{[g]} \in E_f(\bar{\mathbb{Q}})_{\mathbb{Q}}, \end{align*}$$
$$\begin{align*}P_{[g]}^f(e)=\pi_f(\Pi_{m_{[g]}t_{[g]},*}(\Delta_{\operatorname{\mathrm{GKS}}}(e)))\otimes 1/m_{[g]} \in E_f(\bar{\mathbb{Q}})_{\mathbb{Q}}, \end{align*}$$
where
![]() $m_{[g]}$
is the denominator of
$m_{[g]}$
is the denominator of
![]() $\operatorname {\mathrm {pr}}_{[g]}$
.
$\operatorname {\mathrm {pr}}_{[g]}$
.
Building on the work of Yuan et al. [Reference Yuan, Zhang and Zhang28], Darmon et al. proved the following in [Reference Darmon, Rotger and Sols7]:
Theorem 5.3 Assume that
![]() $g\neq f$
,
$g\neq f$
,
![]() $W(f)=-1$
, and
$W(f)=-1$
, and
![]() $W(\operatorname {\mathrm {Sym}}^2 g\otimes f)=+1$
. The subspace
$W(\operatorname {\mathrm {Sym}}^2 g\otimes f)=+1$
. The subspace
 $$\begin{align*}\langle P_{T}^f(\xi_\infty) \: \colon \: T\in \operatorname{\mathrm{CH}}^1(X^2)[g]_{\mathbb{Q}}\rangle \subset E_f(\mathbb{Q})_{\mathbb{Q}} \end{align*}$$
$$\begin{align*}\langle P_{T}^f(\xi_\infty) \: \colon \: T\in \operatorname{\mathrm{CH}}^1(X^2)[g]_{\mathbb{Q}}\rangle \subset E_f(\mathbb{Q})_{\mathbb{Q}} \end{align*}$$
is nonzero if and only if
 $$\begin{align*}\operatorname{\mathrm{ord}}_{s=1} L(f, s)=1 \quad \text{ and } \quad \operatorname{\mathrm{ord}}_{s=2} L(\operatorname{\mathrm{Sym}}^2 (g^\sigma)\otimes f, s)=0, \quad \forall \:\sigma : K_g \hookrightarrow \mathbb{C}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ord}}_{s=1} L(f, s)=1 \quad \text{ and } \quad \operatorname{\mathrm{ord}}_{s=2} L(\operatorname{\mathrm{Sym}}^2 (g^\sigma)\otimes f, s)=0, \quad \forall \:\sigma : K_g \hookrightarrow \mathbb{C}. \end{align*}$$
Proof This is a particular case of [Reference Darmon, Rotger and Sols7, Theorem 3.7].▪
Remark 5.4 The triple product L-function attached to
![]() $(g,g,f)$
decomposes as
$(g,g,f)$
decomposes as
and therefore the assumptions of Theorem 5.3 imply in particular that
![]() $W(g,g,f)=-1$
.
$W(g,g,f)=-1$
.
Remark 5.5 When g equals f,
 $(t_f^{\otimes 3})_*(\Delta _{\operatorname {\mathrm {GKS}}}(e))$
is the Gross–Kudla–Schoen cycle in
$(t_f^{\otimes 3})_*(\Delta _{\operatorname {\mathrm {GKS}}}(e))$
is the Gross–Kudla–Schoen cycle in
 $\operatorname {\mathrm {CH}}^2(E_f^3)_0(\mathbb {Q})$
based at
$\operatorname {\mathrm {CH}}^2(E_f^3)_0(\mathbb {Q})$
based at
![]() $\pi _f(e)$
, which is torsion by [Reference Gross and Schoen12, Corollary 4.7]. The resulting Chow–Heegner point is then trivial by (5.2), whence the assumption in Theorem 5.3.
$\pi _f(e)$
, which is torsion by [Reference Gross and Schoen12, Corollary 4.7]. The resulting Chow–Heegner point is then trivial by (5.2), whence the assumption in Theorem 5.3.
In the complementary setting where
![]() $W(g,g,f)=+1$
, we now prove the following:
$W(g,g,f)=+1$
, we now prove the following:
Theorem 5.6 If
![]() $E_f$
admits split multiplicative reduction at p, then
$E_f$
admits split multiplicative reduction at p, then
 $P_{[g]}^f(e)$
is trivial in
$P_{[g]}^f(e)$
is trivial in
![]() $E_f(\mathbb {Q})_{\mathbb {Q}}$
, for all
$E_f(\mathbb {Q})_{\mathbb {Q}}$
, for all
![]() $e\in X(\mathbb {Q})$
. Equivalently,
$e\in X(\mathbb {Q})$
. Equivalently,
 $m_{[g]}^2P_{[g]}^f(e)$
is torsion in
$m_{[g]}^2P_{[g]}^f(e)$
is torsion in
![]() $E_f(\mathbb {Q})$
, for all
$E_f(\mathbb {Q})$
, for all
![]() $e\text{ in } X(\mathbb {Q})$
.
$e\text{ in } X(\mathbb {Q})$
.
Proof Following Section 2.2, we have
![]() $t_{[g]}=\sum _{h\in [g]} t_h$
, and thus
$t_{[g]}=\sum _{h\in [g]} t_h$
, and thus
 $$\begin{align*}t_{[g]}\otimes t_{[g]} \otimes t_{f}=\sum_{h_1, h_2\in [g]} t_{h_1}\otimes t_{h_2} \otimes t_{f}. \end{align*}$$
$$\begin{align*}t_{[g]}\otimes t_{[g]} \otimes t_{f}=\sum_{h_1, h_2\in [g]} t_{h_1}\otimes t_{h_2} \otimes t_{f}. \end{align*}$$
By (3.2), for any
![]() $h_1, h_2\in [g]$
, the global root number of the triple product L-function
$h_1, h_2\in [g]$
, the global root number of the triple product L-function
![]() $L(h_1,h_2,f, s)$
is given by
$L(h_1,h_2,f, s)$
is given by
![]() $W(h_1, h_2, f)=a_p(h_1)a_p(h_2)a_p(f)$
. The pth Fourier coefficient of a normalized cuspidal eigenform is the negative of the
$W(h_1, h_2, f)=a_p(h_1)a_p(h_2)a_p(f)$
. The pth Fourier coefficient of a normalized cuspidal eigenform is the negative of the
![]() $w_p$
-eigenvalue of the form, hence it belongs to
$w_p$
-eigenvalue of the form, hence it belongs to
![]() $\{ \pm 1 \}$
. In particular, since this coefficient belongs to
$\{ \pm 1 \}$
. In particular, since this coefficient belongs to
![]() $\mathbb {Q}$
, it is fixed by the action of
$\mathbb {Q}$
, it is fixed by the action of
![]() $\mathrm {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})$
, and thus
$\mathrm {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})$
, and thus
![]() $a_p(g)=a_p(h_1)=a_p(h_2)\in \{ \pm 1 \}$
. It follows that
$a_p(g)=a_p(h_1)=a_p(h_2)\in \{ \pm 1 \}$
. It follows that
![]() $W(h_1, h_2, f)=a_p(f)=a_p(E_f)$
. We have
$W(h_1, h_2, f)=a_p(f)=a_p(E_f)$
. We have
![]() $a_p(E_f)=1$
, since
$a_p(E_f)=1$
, since
![]() $E_f$
admits split multiplicative reduction at p, and the triple
$E_f$
admits split multiplicative reduction at p, and the triple
![]() $(h_1,h_2, f)$
satisfies Assumption 4.1. By Theorem 4.3, for any
$(h_1,h_2, f)$
satisfies Assumption 4.1. By Theorem 4.3, for any
![]() $e\in X(\mathbb {Q})$
,
$e\in X(\mathbb {Q})$
,
![]() $\operatorname {\mathrm {AJ}}_{X^3}((t_{h_1}\otimes t_{h_2} \otimes t_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(e)))$
is trivial in the intermediate Jacobian. Thus,
$\operatorname {\mathrm {AJ}}_{X^3}((t_{h_1}\otimes t_{h_2} \otimes t_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(e)))$
is trivial in the intermediate Jacobian. Thus,
![]() $\operatorname {\mathrm {AJ}}_{X^3}((t_{[g]} \otimes t_{[g]} \otimes t_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(e)))$
is trivial in
$\operatorname {\mathrm {AJ}}_{X^3}((t_{[g]} \otimes t_{[g]} \otimes t_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(e)))$
is trivial in
![]() $J^2(X^3_{\mathbb {C}})_{\mathbb {Q}}$
, or equivalently,
$J^2(X^3_{\mathbb {C}})_{\mathbb {Q}}$
, or equivalently,
![]() $\operatorname {\mathrm {AJ}}_{X^3}((m_{[g]}t_{[g]} \otimes m_{[g]}t_{[g]} \otimes m_ft_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(e)))$
is torsion in
$\operatorname {\mathrm {AJ}}_{X^3}((m_{[g]}t_{[g]} \otimes m_{[g]}t_{[g]} \otimes m_ft_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(e)))$
is torsion in
![]() $J^2(X^3_{\mathbb {C}})$
.
$J^2(X^3_{\mathbb {C}})$
.
Define the cycle
 $ \Pi :=\operatorname {\mathrm {pr}}_{12}^*(\Delta )\cdot \operatorname {\mathrm {pr}}_{34}^*(\Delta )\in \operatorname {\mathrm {CH}}^2(X^4)(\mathbb {Q}). $
Viewing
$ \Pi :=\operatorname {\mathrm {pr}}_{12}^*(\Delta )\cdot \operatorname {\mathrm {pr}}_{34}^*(\Delta )\in \operatorname {\mathrm {CH}}^2(X^4)(\mathbb {Q}). $
Viewing
![]() $m_{[g]}t_{[g]} \otimes m_{[g]}t_{[g]} \otimes m_ft_{f}$
in
$m_{[g]}t_{[g]} \otimes m_{[g]}t_{[g]} \otimes m_ft_{f}$
in
![]() $\mathrm {Corr}^0(X^3, X^3)(\mathbb {Q})$
and
$\mathrm {Corr}^0(X^3, X^3)(\mathbb {Q})$
and
![]() $\Pi $
in
$\Pi $
in
![]() $\mathrm {Corr}^{-1}(X^3, X)(\mathbb {Q})$
, we compute
$\mathrm {Corr}^{-1}(X^3, X)(\mathbb {Q})$
, we compute
 $$\begin{align*}\Pi \circ (m_{[g]}t_{[g]} \otimes m_{[g]}t_{[g]} \otimes m_ft_{f}) &= \operatorname{\mathrm{pr}}_{12}^*(m_{[g]}t_{[g]} \circ m_{[g]}t_{[g]})\cdot \operatorname{\mathrm{pr}}_{34}^*(m_ft_f) \\ &= m_{[g]}\Pi_{m_{[g]}t^{\prime}_{[g]},t_f}, \end{align*}$$
$$\begin{align*}\Pi \circ (m_{[g]}t_{[g]} \otimes m_{[g]}t_{[g]} \otimes m_ft_{f}) &= \operatorname{\mathrm{pr}}_{12}^*(m_{[g]}t_{[g]} \circ m_{[g]}t_{[g]})\cdot \operatorname{\mathrm{pr}}_{34}^*(m_ft_f) \\ &= m_{[g]}\Pi_{m_{[g]}t^{\prime}_{[g]},t_f}, \end{align*}$$
as elements of
![]() $\mathrm {Corr}^{-1}(X^3, X)(\mathbb {Q})$
, where
$\mathrm {Corr}^{-1}(X^3, X)(\mathbb {Q})$
, where
 $t^{\prime }_{[g]}$
is possibly another
$t^{\prime }_{[g]}$
is possibly another
![]() $[g]$
-projector arising from the fact that
$[g]$
-projector arising from the fact that
![]() $t_{[g]}$
is an idempotent element of the ring of self-correspondences modulo vertical and horizontal divisors. We deduce the equality of points in
$t_{[g]}$
is an idempotent element of the ring of self-correspondences modulo vertical and horizontal divisors. We deduce the equality of points in
![]() $E_f(\mathbb {Q})_{\mathbb {Q}}$
$E_f(\mathbb {Q})_{\mathbb {Q}}$
 $$ \begin{align} \Pi_*(m_{[g]}t_{[g]} \otimes m_{[g]}t_{[g]} \otimes m_ft_{f})_*(\Delta_{\operatorname{\mathrm{GKS}}}(e))\otimes 1/m_{[g]}^2 =P_{[g]}^f(e). \end{align} $$
$$ \begin{align} \Pi_*(m_{[g]}t_{[g]} \otimes m_{[g]}t_{[g]} \otimes m_ft_{f})_*(\Delta_{\operatorname{\mathrm{GKS}}}(e))\otimes 1/m_{[g]}^2 =P_{[g]}^f(e). \end{align} $$
By functoriality of Abel–Jacobi maps with respect to correspondences, the diagram

commutes. Here,
 $J^1(E_{f,\mathbb {C}})=H^0(E_f(\mathbb {C}), \Omega ^1_{E_f})^\vee / \operatorname {\mathrm {Im}} H_1(E_f(\mathbb {C}), \mathbb {Z})$
is the Jacobian of
$J^1(E_{f,\mathbb {C}})=H^0(E_f(\mathbb {C}), \Omega ^1_{E_f})^\vee / \operatorname {\mathrm {Im}} H_1(E_f(\mathbb {C}), \mathbb {Z})$
is the Jacobian of
![]() $E_f$
, and
$E_f$
, and
![]() $\operatorname {\mathrm {AJ}}_{E_f}$
is the classical Abel–Jacobi isomorphism for the elliptic curve
$\operatorname {\mathrm {AJ}}_{E_f}$
is the classical Abel–Jacobi isomorphism for the elliptic curve
![]() $E_f$
given by
$E_f$
given by
 $$\begin{align*}\operatorname{\mathrm{AJ}}_{E_f}(P)(\alpha):= \int_{\mathcal{O}}^P \alpha, \quad \text{ for all } \alpha\in H^0(E_f(\mathbb{C}), \Omega^1_{E_f}), \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{AJ}}_{E_f}(P)(\alpha):= \int_{\mathcal{O}}^P \alpha, \quad \text{ for all } \alpha\in H^0(E_f(\mathbb{C}), \Omega^1_{E_f}), \end{align*}$$
where
![]() $\mathcal {O}$
is the origin of
$\mathcal {O}$
is the origin of
![]() $E_f$
. By (5.2) and (5.3), we have the equality in
$E_f$
. By (5.2) and (5.3), we have the equality in
 $J^1(E_{f,\mathbb {C}})$
$J^1(E_{f,\mathbb {C}})$
 $$ \begin{align} \operatorname{\mathrm{AJ}}_{E_f}(m_{[g]}^2P_{[g]}^f(e)) = (\Pi^*)^\vee \operatorname{\mathrm{AJ}}_{X^3}((m_{[g]}t_{[g]} \otimes m_{[g]}t_{[g]} \otimes m_ft_{f})_*(\Delta_{\operatorname{\mathrm{GKS}}}(e))). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{AJ}}_{E_f}(m_{[g]}^2P_{[g]}^f(e)) = (\Pi^*)^\vee \operatorname{\mathrm{AJ}}_{X^3}((m_{[g]}t_{[g]} \otimes m_{[g]}t_{[g]} \otimes m_ft_{f})_*(\Delta_{\operatorname{\mathrm{GKS}}}(e))). \end{align} $$
The result follows from the facts that
![]() $\operatorname {\mathrm {AJ}}_{X^3}((m_{[g]}t_{[g]} \otimes m_{[g]}t_{[g]} \otimes m_ft_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(e)))$
is torsion and
$\operatorname {\mathrm {AJ}}_{X^3}((m_{[g]}t_{[g]} \otimes m_{[g]}t_{[g]} \otimes m_ft_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(e)))$
is torsion and
![]() $\operatorname {\mathrm {AJ}}_{E_f}$
is an isomorphism.▪
$\operatorname {\mathrm {AJ}}_{E_f}$
is an isomorphism.▪
Remark 5.7 Theorem 5.6 with
![]() $e=\xi _\infty $
is a special case of [Reference Daub8, Theorem 3.3.8]. In his thesis [Reference Daub8], Daub proved more generally for composite level N that if the local root number
$e=\xi _\infty $
is a special case of [Reference Daub8, Theorem 3.3.8]. In his thesis [Reference Daub8], Daub proved more generally for composite level N that if the local root number
![]() $W_p(g,g,f)=-1$
for some
$W_p(g,g,f)=-1$
for some
![]() $p \: \vert \: N$
, then the resulting Chow–Heegner points based at
$p \: \vert \: N$
, then the resulting Chow–Heegner points based at
![]() $\xi _\infty $
are torsion. His proof relies on an identification of these points with Zhang points [Reference Zhang29]. As explained in the introduction (Section 1.4), our method works for composite level N.
$\xi _\infty $
are torsion. His proof relies on an identification of these points with Zhang points [Reference Zhang29]. As explained in the introduction (Section 1.4), our method works for composite level N.
6 Example of a nontrivial torsion element
Techniques were developed in [Reference Darmon, Daub, Lichtenstein and Rotger5] to numerically calculate Chow–Heegner points associated with modified diagonal cycles. The algorithms are based on a formula for the image of these cycles under the complex Abel–Jacobi map (4.1) proved in [Reference Darmon, Rotger and Sols7]. Most of the examples calculated in [Reference Darmon, Daub, Lichtenstein and Rotger5] concern the situation where the elliptic curve
![]() $E_f$
has algebraic rank equal to
$E_f$
has algebraic rank equal to
![]() $1$
. In particular, the global root number of
$1$
. In particular, the global root number of
![]() $E_f$
is
$E_f$
is
![]() $-1$
, and this is not the setting studied in the present paper. However, in the appendix of [Reference Darmon, Daub, Lichtenstein and Rotger5] by Stein, some examples are computed for which the rank of
$-1$
, and this is not the setting studied in the present paper. However, in the appendix of [Reference Darmon, Daub, Lichtenstein and Rotger5] by Stein, some examples are computed for which the rank of
![]() $E_f$
is
$E_f$
is
![]() $0$
. In particular, we deduce the following:
$0$
. In particular, we deduce the following:
Theorem 6.1 Let f and g be the normalized eigenforms of weight
![]() $2$
and level
$2$
and level
![]() $\Gamma _0(37)$
corresponding to the elliptic curves with Cremona labels
$\Gamma _0(37)$
corresponding to the elliptic curves with Cremona labels
![]() $37$
b and
$37$
b and
![]() $37$
a, and define
$37$
a, and define
![]() $F:=g\otimes g\otimes f$
. Then
$F:=g\otimes g\otimes f$
. Then
![]() $\operatorname {\mathrm {AJ}}_{X_0(37)^3}((2t_{g} \otimes 2t_{g} \otimes 2t_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty )))$
is a nontrivial
$\operatorname {\mathrm {AJ}}_{X_0(37)^3}((2t_{g} \otimes 2t_{g} \otimes 2t_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty )))$
is a nontrivial
![]() $6$
-torsion element of
$6$
-torsion element of
![]() $J^2(X_0(37)^3_{\mathbb {C}})$
.
$J^2(X_0(37)^3_{\mathbb {C}})$
.
Proof In [Reference Darmon, Daub, Lichtenstein and Rotger5, Appendix], it is verified numerically in this case that
 $m_{g}P_{g}^f(\xi _\infty )$
is a point of order
$m_{g}P_{g}^f(\xi _\infty )$
is a point of order
![]() $3$
in
$3$
in
![]() $E_f(\mathbb {Q})$
. By inspecting the first few Fourier coefficients of f and g, we see that
$E_f(\mathbb {Q})$
. By inspecting the first few Fourier coefficients of f and g, we see that
![]() $m_g=m_f=2$
(see [Reference Darmon, Daub, Lichtenstein and Rotger5, Section 5.1]). The point
$m_g=m_f=2$
(see [Reference Darmon, Daub, Lichtenstein and Rotger5, Section 5.1]). The point
 $4P_{g}^f(\xi _\infty )\in E_f(\mathbb {Q})$
has order
$4P_{g}^f(\xi _\infty )\in E_f(\mathbb {Q})$
has order
![]() $3$
, and by (5.4)
$3$
, and by (5.4)
![]() $\operatorname {\mathrm {AJ}}_{X_0(37)^3}((2t_{g} \otimes 2t_{g} \otimes 2t_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty )))$
is thus nontrivial in
$\operatorname {\mathrm {AJ}}_{X_0(37)^3}((2t_{g} \otimes 2t_{g} \otimes 2t_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty )))$
is thus nontrivial in
![]() $J^2(X_0(37)_{\mathbb {C}}^3)$
.
$J^2(X_0(37)_{\mathbb {C}}^3)$
.
The element
![]() $ 2\operatorname {\mathrm {AJ}}_{X_0(37)^3}((2t_{g} \otimes 2t_{g} \otimes 2t_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty )))$
is equal by Proposition 4.6 to
$ 2\operatorname {\mathrm {AJ}}_{X_0(37)^3}((2t_{g} \otimes 2t_{g} \otimes 2t_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty )))$
is equal by Proposition 4.6 to
![]() $\operatorname {\mathrm {AJ}}_{X_0(37)^3}((2t_{g} \otimes 2t_{g} \otimes 2t_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty )-\Delta _{\operatorname {\mathrm {GKS}}}(\xi _0)))$
, and depends only on the class of
$\operatorname {\mathrm {AJ}}_{X_0(37)^3}((2t_{g} \otimes 2t_{g} \otimes 2t_{f})_*(\Delta _{\operatorname {\mathrm {GKS}}}(\xi _\infty )-\Delta _{\operatorname {\mathrm {GKS}}}(\xi _0)))$
, and depends only on the class of
![]() $(\xi _\infty )-(\xi _0)$
in
$(\xi _\infty )-(\xi _0)$
in
![]() $J_0(37)(\mathbb {Q})$
by existence of (4.5). The latter has order
$J_0(37)(\mathbb {Q})$
by existence of (4.5). The latter has order
![]() $3$
[Reference Mazur21, Theorem 1].▪
$3$
[Reference Mazur21, Theorem 1].▪
Acknowledgment
The author thanks H. Darmon, B. H. Gross, and A. Shnidman for helpful comments, as well as C. Qiu and W. Zhang for answering questions related to their work. The author was supported by the Institut des Sciences Mathématiques at McGill University, and by an Emily Erskine Endowment Fund Postdoctoral Fellowship at the Hebrew University. The author thanks the anonymous referee for their valuable feedback and suggestions.