Hostname: page-component-5cf477f64f-mgq6s Total loading time: 0 Render date: 2025-04-08T08:24:46.113Z Has data issue: false hasContentIssue false
  • English
  • Français

Toric degenerations of low-degree hypersurfaces

Part of: Surfaces and higher-dimensional varieties Computational aspects and applications Special varieties

Published online by Cambridge University Press:  20 April 2023

Nathan Ilten  and
Oscar Lautsch
Nathan Ilten*
Affiliation:
Department of Mathematics, Simon Fraser University, 8888 University Drive, Burnaby, BC V5A 1S6, Canada e-mail: [email protected]
Oscar Lautsch
Affiliation:
Department of Mathematics, Simon Fraser University, 8888 University Drive, Burnaby, BC V5A 1S6, Canada e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that a sufficiently general hypersurface of degree d in 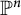$\mathbb {P}^n$ admits a toric Gröbner degeneration after linear change of coordinates if and only if 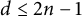$d\leq 2n-1$.

Keywords

Toric degenerationhypersurfacesKhovanskii basis

MSC classification

Primary: 13P10: Gröbner bases; other bases for ideals and modules (e.g., Janet and border bases) 14J70: Hypersurfaces 14M25: Toric varieties, Newton polyhedra
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 4 , December 2023 , pp. 1231 - 1236
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

N.I. was supported by an NSERC Discovery Grant. O.L. was supported by an NSERC undergraduate student research award.

References

Anderson, D., Okounkov bodies and toric degenerations . Math. Ann. 356(2013), no. 3, 1183–1202.CrossRefGoogle Scholar
Bossinger, L., Lamboglia, S., Mincheva, K., and Mohammadi, F., Computing toric degenerations of flag varieties . In: Smith, G. and Sturmfels, B. (eds.), Combinatorial algebraic geometry, vol. 80 of Fields Institute Communications, Fields Institute for Research in Mathematical Sciences, Toronto, ON, 2017, pp. 247–281.CrossRefGoogle Scholar
Coates, T., Corti, A., Galkin, S., Golyshev, V., and Kasprzyk, A., Mirror symmetry and Fano manifolds . In: European Congress of Mathematics, European Mathematical Society, Zürich, 2013, pp. 285–300.Google Scholar
Harada, M. and Kaveh, K., Integrable systems, toric degenerations and Okounkov bodies . Invent. Math. 202(2015), no. 3, 927–985.CrossRefGoogle Scholar
Ito, A., Seshadri constants via toric degenerations . J. Reine Angew. Math. 695(2014), 151–174.CrossRefGoogle Scholar
Kaveh, K. and Manon, C., Khovanskii bases, higher rank valuations, and tropical geometry . SIAM J. Appl. Algebra Geom. 3(2019), no. 2, 292–336.CrossRefGoogle Scholar
Kaveh, K., Manon, C., and Murata, T., Generic tropical initial ideals of Cohen–Macaulay algebras. J. Pure Appl. Algebra, 225(2021), no. 11, 106713. https://doi.org/10.1016/j.jpaa.2021.106713CrossRefGoogle Scholar
Kaveh, K., Manon, C., and Murata, T., On degenerations of projective varieties to complexity-one $T$ -varieties . Int. Math. Res. Not. IMRN. 2023(2023), no. 3, 2665–2697.CrossRefGoogle Scholar
Maclagan, D. and Sturmfels, B., Introduction to tropical geometry, vol. 161, Graduate Studies in Mathematics, American Mathematical Society, Providence, RI, 2015.CrossRefGoogle Scholar