Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T04:03:44.554Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological Quantum Field Theory and Strong Shift Equivalence

Published online by Cambridge University Press:  20 November 2018

Patrick M. Gilmer
Patrick M. Gilmer*
Affiliation:
Department of Mathematics Louisiana State University Baton Rouge, Louisiana 70803 USA, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a 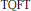$\text{TQFT}$ in dimension 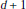$d\,+\,1$, and an infinite cyclic covering of a closed (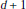$d\,+\,1$)-dimensional manifold 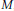$M$, we define an invariant taking values in a strong shift equivalence class of matrices. The notion of strong shift equivalence originated in R. Williams’ work in symbolic dynamics. The Turaev-Viro module associated to a 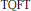$\text{TQFT}$ and an infinite cyclic covering is then given by the Jordan form of this matrix away from zero. This invariant is also defined if the boundary of 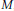$M$ has an ${{S}^{1}}$ factor and the infinite cyclic cover of the boundary is standard. We define a variant of a 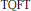$\text{TQFT}$ associated to a finite group 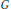$G$ which has been studied by Quinn. In this way, we recover a link invariant due to D. Silver and S. Williams. We also obtain a variation on the Silver-Williams invariant, by using the 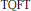$\text{TQFT}$ associated to 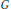$G$ in its unmodified form.

Keywords

57R9957M9954H20knotlinkTQFTsymbolic dynamicsshift equivalence
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 2 , 01 June 1999 , pp. 190 - 197
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Bar-Natan, D., Fulman, J. and Kauffman, L., An Elementary Proof that all Seifert Surfaces of a link are Tubeequivalent. Preprint.Google Scholar
[2] Blanchet, C., Habegger, N., Masbaum, G. and Vogel, P., Topological quantum field theories derived from the Kauffman bracket. Topology 34 (1995), 883–927.Google Scholar
[3] Freed, D. and Quinn, F., Chern-Simons Theory with Finite Gauge Group. Commun. Math. Phys. 156 (1993), 435–472.Google Scholar
[4] Gilmer, P., Invariants for 1-dimensional cohomology classes arising from TQFT. Topology Appl. 75 (1997), 217–259.Google Scholar
[5] Gilmer, P., Turaev-Viro Modules of Satellite Knots. In: Knots 96 (Ed. S. Suzuki), World Scientific, 1997, 337– 363.Google Scholar
[6] Gordon, C. McA. and Litherland, R., On the Signature of a link. Invent.Math. 47 (1978), 53–69.Google Scholar
[7] Lind, D. and Marcus, B., An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, 1995.Google Scholar
[8] Massey, W., Algebraic Topology—an introduction. Springer, 1967.Google Scholar
[9] Silver, D. and Williams, S., Augmented Group Systems and Shifts of Finite Type. Israel J. Math. 95 (1996), 231–251.Google Scholar
[10] Silver, D. and Williams, S., Knot Invariants from Symbolic Dynamical Systems. Trans. Amer.Math. Soc., to appear.Google Scholar
[11] Silver, D. and Williams, S., Generalized n-colorings of links. In: Knot Theory (Eds. V. F. R. Jones, J. Kania-Bartoszynska, J. H. Przytycki, P. Traczyk and V. Turaev), Banach Center Publications 42, Warsaw, 1995, to appear.Google Scholar
[12] Silver, D. and Williams, S., Knots, Links and Representation Shifts. 13th Annual Western Workshop on Geometric Topology, The Colorado College, 1996.Google Scholar
[13] Stevens, W., On the homology of branched cyclic covers of knots. LSU Ph.D. dissertation, August, 1996.Google Scholar
[14] Stevens, W., Periodicity For Zpr-Homology of cyclic covers of knots and Z-homology circles. J. Pure Applied Algebra, to appear.Google Scholar
[15] Turaev, V., Quantum Invariants of Knots and 3-manifolds. De Gruyer, 1994.Google Scholar
[16] Quinn, F., Lectures on Axiomatic Topological Quantum Field Theory. In: Geometry and Quantum Field Theory (Eds. D. Freed and K. Uhlenbeck), Park City Utah 1991, Amer. Math. Soc., 1995.Google Scholar
[17] Williams, R. F., Classification of subshifts of finite type. Ann. of Math. 98 (1973), 120–153; Errata, ibid. 99 (1974), 380–381.Google Scholar