Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-30T19:52:43.522Z Has data issue: false hasContentIssue false
  • English
  • Français

The Topological Interpretation of the Core Group of a Surface in S4

Published online by Cambridge University Press:  20 November 2018

Józef H. Przytycki  and
Witold Rosicki
Józef H. Przytycki
Affiliation:
Department of Mathematics, George Washington University and University of Maryland, College Park, email: [email protected]
Witold Rosicki
Affiliation:
Institute of Mathematics, Gdańsk University, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a topological interpretation of the core group invariant of a surface embedded in 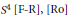${{S}^{4}}\,\left[ \text{F-R} \right],\,\left[ \text{Ro} \right]$. We show that the group is isomorphic to the free product of the fundamental group of the double branch cover of 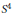${{S}^{4}}$ with the surface as a branched set, and the infinite cyclic group. We present a generalization for unoriented surfaces, for other cyclic branched covers, and other codimension two embeddings of manifolds in spheres.

Keywords

57Q4557M1257M05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 1 , 01 March 2002 , pp. 131 - 137
Copyright
Copyright © Canadian Mathematical Society 2002

References

[CJKLS] Carter, J. S., Jelsovsky, D., Kamada, S., Langford, L. and Saito, M., Quandle cohomology and state-sum invariants of knotted curves and surfaces. Preprint, April 1999.Google Scholar
[C-S-1] Carter, J. S. and Saito, M., Knot diagrams and braid theories in dimension 4. Real and complex singularities (São Carlos, 1994), Pitman Res. Notes Math. Ser. 333, Longman, Harlow, 1995, 112–147.Google Scholar
[C-S-2] Carter, J. S. and Saito, M., Knotted surfaces and their diagrams. Math. SurveysMonographs 55, Amer.Math. Soc., Providence, RI, 1998.Google Scholar
[F-R] Fenn, R. and Rourke, C., Racks and links in codimension two. J. Knot Theory Ramifications (4) 1 (1992), 343–406.Google Scholar
[Joy] Joyce, D., A classifying invariant of knots: the knot quandle. J. Pure Appl. Algebra 23 (1982), 37–65.Google Scholar
[Ka-1] Kamada, S., A characterization of groups of closed orientable surfaces in 4-space. Topology (1) 33 (1994), 113–122.Google Scholar
[Ka-2] Kamada, S., Wirtinger presentations for higher dimensional manifold knots obtained from diagrams. Preprint, 1999.Google Scholar
[Pr] Przytycki, J. H., 3-coloring and other elementary invariants of knots. Knot Theory (Warsaw, 1995), Banach Center Publications 42 (1998), 275–295.Google Scholar
[Ros-1] Roseman, D., Reidemeister-type moves for surfaces in four-dimensional space. Knot Theory (Warsaw, 1995), Banach Center Publications 42 (1998), 347–380.Google Scholar
[Ros-2] Roseman, D., Projections of codimension two embeddings. Knots in Hellas’98, Series on Knots and Everything, Vol. 24, Proceedings of the International Conference on Knot Theory and its Ramifications (Delphi, 1998), World Scientific, September 2000, 380–410.Google Scholar
[Ro] Rosicki, W., Some simple invariants of the position of a surface in R4. Bull. Polish Acad. Sci. Math. (4) 46 (1998), 335–344.Google Scholar
[Wa] Wada, M., Group invariants of links. Topology (2) 31 (1992), 399–406.Google Scholar
[Ya-1] Yajima, T., On the fundamental groups of knotted 2-manifolds in the 4-space. J. Math. Osaka City Univ. 13 (1962), 63–71.Google Scholar
[Ya-2] Yajima, T., Wirtinger presentations of knot groups. Proc. Japan Acad. (10) 46(1970), suppl. to (9) 46 (1970), 997–1000.Google Scholar
[Yo] Yoshikawa, K., The order of a meridian of unknotted Klein bottle. Proc. Amer.Math. Soc. 126 (1998), 3727–3731.Google Scholar