Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T05:57:08.808Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological Games and Alster Spaces

Published online by Cambridge University Press:  20 November 2018

Leandro F. Aurichi  and
Rodrigo R. Dias
Leandro F. Aurichi
Affiliation:
Instituto de Ciências Matemáticas e de Computaçao, Universidade de São Paulo, Caixa Postal 668, Sāo Carlos, SP, 13560-970, Brazil e-mail: [email protected]
Rodrigo R. Dias
Affiliation:
Instituto de Matemática e Estatística, Universidade de Paulo, Caixa Postal 66281, Paulo, SP, 05315- 970, Brazil e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study connections between topological games such as Rothberger, Menger, and compact-open games, and we relate these games to properties involving covers by 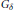${{G}_{\delta }}$ subsets. The results include the following: (1) If TWO has a winning strategy in theMenger game on a regular space 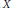$X$, then 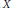$X$ is an Alster space. (2) If TWO has a winning strategy in the Rothberger game on a topological space 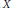$X$, then the 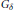${{G}_{\delta }}$-topology on 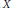$X$ is Lindelöf. (3) The Menger game and the compact-open game are (consistently) not dual.

Keywords

54D2054G9954A10topological gamesselection principlesAlster spacesMenger spacesRothberger spacesMenger gameRothberger gamecompact-open gameGδ-topology
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 4 , 01 December 2014 , pp. 683 - 696
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Alster, K., On the class of all spaces of weight not greater than 1 whose cartesian product with every Lindelöf space is Lindelöf.Fund. Math. 129 (1988), no. 2, 133–140.Google Scholar
[2] Arkhangel’skii, A. V., On some topological spaces that occur in functional analysis.(Russian) Uspehi Mat. Nauk 31 (1976), no. 5, 17–32.Google Scholar
[3] Aurichi, L. F., D-spaces, topological games, and selection principles.Topology Proc. 36 (2010), 107–122.Google Scholar
[4] Babinkostova, L., Pansera, B. A., and Scheepers, M., Weak covering properties and selection principles.Topology Applic. 160 (2013), no. 18, 2251–2271. http://dx.doi.org/10.1016/j.topol.2013.07.022 Google Scholar
[5] Banakh, T. and Zdomskyy, L., Selection principles and infinite games on multicovered spaces. In: Selection principles and covering properties in topology, Quad. Mat., 18, Dept. Math., Seconda UniNapoli, v., Caserta, 2006, pp. 1–51.Google Scholar
[6] Barr, M., Kennison, J. F., and Raphael, R., On productively Lindelöf spaces.Sci. Math. Jpn. 65 (2007), no. 3, 319–332.Google Scholar
[7] Bartoszynski, T. and Tsaban, B., Hereditary topological diagonalizations and the Menger-Hurewicz conjectures. Proc. Amer. Math. Soc. 134 (2006), no. 2, 605–615. http://dx.doi.org/10.1090/S0002-9939-05-07997-9 Google Scholar
[8] Č ech, E. and B. Posp´ısˇil, Sur les espaces compacts.Publ. Fac. Sci. Univ. Masaryk 258 (1938), 1–7.Google Scholar
[9] Dow, A., An introduction to applications of elementary submodels to topology.Topology Proc. 13 (1988), no. 1, 17–72.Google Scholar
[10] Fodor, G., Eine Bemerkung zur Theorie der regressiven Funktionen.Acta Sci. Math. Szeged 17 (1956), 139–142.Google Scholar
[11] Fremlin, D. H. and A.Miller, W., On some properties of Hurewicz, Menger, and Rothberger.Fund. Math. 129 (1988), no. 1, 17–33.Google Scholar
[12] Galvin, F., Indeterminacy of point-open games.Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 26 (1978), 445–449.Google Scholar
[13] Gerlits, J. and Nagy, Z., Some properties of C(X). I.Topology Appl. 14 (1982), no. 2, 151–161. http://dx.doi.org/10.1016/0166-8641(82)90065-7 Google Scholar
[14] Hodel, R., Cardinal functions. I. In: Handbook of set-theoretic topology, North-Holland, Amsterdam, 1984, pp. 1–61.Google Scholar
[15] Hurewicz, W., Über eine Verallgemeinerung des Borelschen Theorems.Math. Z. 24 (1926), no. 1. 401–421. http://dx.doi.org/10.1007/BF01216792 Google Scholar
[16] Hurewicz, W., Über Folgen stetiger Funktionen.Fund. Math. 9 (1927), 193–204.Google Scholar
[17] Just, W. and M.Weese, Discovering modern set theory. II. Set-theoretic tools for every mathematician. Graduate Studies in Mathematics, 18, American Mathematical Society, Providence, RI, 1997.Google Scholar
[18] Lawrence, L. B., The influence of a small cardinal on the product of a Lindelöf space and the irrationals.Proc. Amer. Math. Soc. 110 (1990), no. 2, 535–542.Google Scholar
[19] Lusin, N., Sur un probláme de M. Baire.C. R. Acad. Sci. Paris 158 (1914), 1258–1261.Google Scholar
[20] Michael, E. A., Paracompactness and the Lindelöf property in finite and countable cartesian products.Compos. Math. 23 (1971), 199–214.Google Scholar
[21] Moore, J. T., Some of the combinatorics related to Michael's problem.Proc. Amer. Math. Soc. 127 (1999), no. 8, 2459–2467. http://dx.doi.org/10.1090/S0002-9939-99-04808-X Google Scholar
[22] , A solution to the L space problem. J. Amer. Math. Soc. 19 (2006), no. 3, 717–736. http://dx.doi.org/10.1090/S0894-0347-05-00517-5 Google Scholar
[23] Pawlikowski, J., Undetermined sets of point-open games. Fund. Math. 144 (1994), no. 3, 279–285.Google Scholar
[24] Przymusiński, T. C., Products of normal spaces. In: Handbook of set-theoretic topology, North-Holland, Amsterdam, 1984, pp. 781–826.Google Scholar
[25] Repovš, D. and Zdomskyy, L., On the Menger covering property and D spaces.Proc. Amer. Math. Soc. 140 (2012), no. 3, 1069–1074. http://dx.doi.org/10.1090/S0002-9939-2011-10945-6 Google Scholar
[26] Rothberger, F., Eine Verschärfung der Eigenschaft C.Fund. Math. 30 (1938), 50–55.Google Scholar
[27] Sakai, M., Menger subsets of the Sorgenfrey line.Proc. Amer. Math. Soc. 137 (2009), no. 9, 3129–3138. http://dx.doi.org/10.1090/S0002-9939-09-09887-6Google Scholar
[28] Scheepers, M., A direct proof of a theorem of Telg´arsky.Proc. Amer. Math. Soc. 123 (1995), no. 11, 3483–3485.Google Scholar
[29] Scheepers, M., Combinatorics of open covers I: Ramsey theory.Topology Appl. 69 (1996), no. 1, 31–62. http://dx.doi.org/10.1016/0166-8641(95)00067-4 Google Scholar
[30] Scheepers, M., Combinatorics of open covers. III. Games, Cp(X). Fund. Math. 152 (1997), no. 3, 231–254.Google Scholar
[31] Scheepers, M., Combinatorics of open covers. VI. Selectors for sequences of dense sets.Quaest. Math. 22 (1999), no. 1, 109–130. http://dx.doi.org/10.1080/16073606.1999.9632063 Google Scholar
[32] Scheepers, M. and Tall, F. D., Lindelöf indestructibility, topological games and selection principles.Fund. Math. 210 (2010), no. 1, 1–46. http://dx.doi.org/10.4064/fm210-1-1 Google Scholar
[33] Sierpinski, W., Sur l’hypotháse du continu (2@0 = @1).Fund. Math. 5 (1924), 177–187.Google Scholar
[34] Tall, F. D., Productively Lindelöf spaces may all be D.Canad. Math. Bull. 56 (2013), no. 1, 203–212. http://dx.doi.org/10.4153/CMB-2011-150-2 Google Scholar
[35] Telgársky, R., Spaces defined by topological games.Fund. Math. 88 (1975), no. 3, 193–223.Google Scholar
[36] Telgársky, R., Spaces defined by topological games. II.Fund. Math. 116 (1983), no. 3, 189–207.Google Scholar
[37] Telgársky, R., On games of Topsøe.Math. Scand. 54 (1984), no. 1, 170–176.Google Scholar
[38] Tsaban, B. and Zdomskyy, L., Arhangel’skiĭ sheaf amalgamations in topological groups. http://arxiv:1103.4957v1 Google Scholar