Article contents
Tight frames and related geometric problems
Published online by Cambridge University Press: 18 December 2020
Abstract
A tight frame is the orthogonal projection of some orthonormal basis of 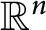 $\mathbb {R}^n$
onto
$\mathbb {R}^n$
onto 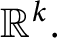 $\mathbb {R}^k.$
We show that a set of vectors is a tight frame if and only if the set of all cross products of these vectors is a tight frame. We reformulate a range of problems on the volume of projections (or sections) of regular polytopes in terms of tight frames and write a first-order necessary condition for local extrema of these problems. As applications, we prove new results for the problem of maximization of the volume of zonotopes.
$\mathbb {R}^k.$
We show that a set of vectors is a tight frame if and only if the set of all cross products of these vectors is a tight frame. We reformulate a range of problems on the volume of projections (or sections) of regular polytopes in terms of tight frames and write a first-order necessary condition for local extrema of these problems. As applications, we prove new results for the problem of maximization of the volume of zonotopes.
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
The author was supported by the Swiss National Science Foundation grant 200021_179133. The author acknowledges the financial support from the Ministry of Education and Science of the Russian Federation in the framework of MegaGrant no. 075-15-2019-1926.
References
- 2
- Cited by



