Hostname: page-component-f554764f5-68cz6 Total loading time: 0 Render date: 2025-04-19T15:02:34.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Three Problems on Exponential Bases

Part of: Nontrigonometric harmonic analysis

Published online by Cambridge University Press:  07 January 2019

Laura De Carli ,
Alberto Mizrahi  and
Alexander Tepper
Laura De Carli
Affiliation:
Department of Mathematics, Florida International University, Miami, FL 33199, USA Email: decarlil@fiu.eduamizr007@fiu.eduatepp001@fiu.edu
Alberto Mizrahi
Affiliation:
Department of Mathematics, Florida International University, Miami, FL 33199, USA Email: decarlil@fiu.eduamizr007@fiu.eduatepp001@fiu.edu
Alexander Tepper
Affiliation:
Department of Mathematics, Florida International University, Miami, FL 33199, USA Email: decarlil@fiu.eduamizr007@fiu.eduatepp001@fiu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider three special and significant cases of the following problem. Let 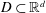$D\subset \mathbb{R}^{d}$ be a (possibly unbounded) set of finite Lebesgue measure. Let $E(\mathbb{Z}^{d})=\{e^{2\unicode[STIX]{x1D70B}ix\cdot n}\}\text{}_{n\in \mathbb{Z}^{d}}$ be the standard exponential basis on the unit cube of $\mathbb{R}^{d}$. Find conditions on 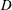$D$ for which 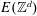$E(\mathbb{Z}^{d})$ is a frame, a Riesz sequence, or a Riesz basis for 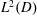$L^{2}(D)$.

Keywords

exponential basisframeRiesz sequencelattice

MSC classification

Primary: 42C15: General harmonic expansions, frames
Secondary: 42C30: Completeness of sets of functions
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 1 , March 2019 , pp. 55 - 70
Copyright
© Canadian Mathematical Society 2018 

References

Ajtai, M., Generating hard instances of lattice problems (extended abstract) . In: Proceedings of the twenty-eighth annual ACM symposium on the theory of computing (Philadelphia, PA, 1996), ACM, New York, 1996, pp. 99–108. https://doi.org/10.1145/237814.237838.Google Scholar
Aggarwal, D. and Dubey, C., Improved hardness results for unique shortest vector problem . Inform. Process. Lett. 116(2016), no. 10, 631–637. https://doi.org/10.1016/j.ipl.2016.05.003.Google Scholar
Aldroubi, A., Sun, Q., and Tang, W., Connection between p–frames and p–Riesz bases in locally finite SIS of L p (ℝ). Proceedings of SPIE: The International Society for Optical Engineering, February 1970.Google Scholar
Aldroubi, A., Sun, Q., and Tang, W., p-Frames and shift invariant subspaces of L p . J. Fourier Anal. Appl. 7(2001), 1–21. https://doi.org/10.1007/s00041-001-0001-2.Google Scholar
Agora, E., Antezana, J., and Cabrelli, C., Multi-tiling sets, Riesz bases, and sampling near the critical density in LCA groups . Adv. Math. 285(2015), 454–477. https://doi.org/10.1016/j.aim.2015.08.006.Google Scholar
Selvan, A. and Radha, R., Sampling and reconstruction in shift invariant spaces on ℝ d . Ann. Mat. Pura Appl. 194(2015), no. 6, 1683–1706. https://doi.org/10.1007/s10231-014-0439-x.Google Scholar
Barbieri, D., Hernandez, E., and Mayeli, A., Lattice sub-tilings and frames in LCA groups . C. R. Math. Acad. Sci. Paris 355(2017), no. 2, 193–199. https://doi.org/10.1016/j.crma.2016.11.017.Google Scholar
Beurling, A., The collected works of Arne Beurling. Vol. 2, Contemporary Mathematics, Birkhäuser Boston Inc., Boston, MA, 1989.Google Scholar
Beurling, A., Local harmonic analysis with some applications to differential operator . In: Some Recent Advances in the Basic Sciences, Vol. 1 (Proc. Annual Sci. Conf., Belfer Grad. School Sci., Yeshiva Univ., New York, 1962–1964), Belfer Graduate School of Science, Yeshiva Univ., New York, 1966, pp. 109–125.Google Scholar
Casazza, P., Christensen, O., and Stoeva, D. T., Frame expansions in separable Banach spaces . J. Math. Anal. Appl. 307(2005), 710–723. https://doi.org/10.1016/j.jmaa.2005.02.015.Google Scholar
Christiansen, O., An introduction to frames and Riesz bases. Applied and numerical harmonic analysis. Birkhäuser Boston, Inc., Boston, MA, 2003. https://doi.org/10.1007/978-0-8176-8224-8.Google Scholar
Christiansen, O., Deng, B., and Heil, C., Density of Gabor frames . Appl. Comput. Harmon. Anal. 7(1999), 292–304. https://doi.org/10.1006/acha.1999.0271.Google Scholar
Christensen, O. and Stoeva, D. T., p-frames in separable Banach spaces . Adv. Comput. Math. 18(2003), 117–126. https://doi.org/10.1023/A:1021364413257.Google Scholar
De Carli, L. and Kumar, A., Exponential bases on two dimensional trapezoids . Proc. Amer. Math. Soc. 143(2015), no. 7, 2893–2903. https://doi.org/10.1090/S0002-9939-2015-12329-5.Google Scholar
Fuglede, B., Commuting self-adjoint partial differential operators and a group theoretic problem . J. Functional Analysis 16(1974), 101–121.Google Scholar
Gabardo, J.-P. and Li, Y.-Z., Density results for Gabor systems associated with periodic subsets of the real line . J. Approx. Theory 157(2009), 172–192. https://doi.org/10.1016/j.jat.2008.08.007.Google Scholar
Grepstad, S. and Lev, N., Multi-tiling and Riesz bases . Adv. Math. 252(2014), 1–6. https://doi.org/10.1016/j.aim.2013.10.019.Google Scholar
Haase, M., Functional analysis: an elementary introduction. Graduate studies in Mathematics, 156, American Mathematical Society, Providence, RI, 2014.Google Scholar
Heil, C., A basis theory primer. Applied and Numerical Harmonic Analysis, Birkhäuser/Springer, New York, 2011. https://doi.org/10.1007/978-0-8176-4687-5.Google Scholar
Khot, S., Hardness of approximating the shortest vector problem in lattices . J. ACM. 52(2005), no. 5, 789–808. https://doi.org/10.1145/1089023.1089027.Google Scholar
Kolountzakis, M., Multiple lattice tiles and Riesz bases of exponentials . Proc. Amer. Math. Soc. 143(2015), 741–747. https://doi.org/10.1090/S0002-9939-2014-12310-0.Google Scholar
Kolountzakis, M., The study of translational tiling with Fourier analysis. Fourier analysis and convexity, Appl. Numer. Harmon. Anal., Birkhäuser Boston, Boston, MA, 2004, pp. 131–187.Google Scholar
Jia, R. Q. and Micchelli, C. A., Using the refinement equation for the construction of pre-wavelets II: power of two . In: Curves and surfaces (Chamonix-Mont-Blanc, 1990), Academic Press, Boston, MA, 1991, pp. 209–246.Google Scholar
Laba, I., Fuglede’s conjecture for a union of two intervals . Proc. Amer. Math. Soc. 129(2001), no. 10, 2965–2972. https://doi.org/10.1090/S0002-9939-01-06035-X.Google Scholar
Landau, H. J., Necessary density conditions for sampling and interpolation of certain entire functions . Acta Math. 117(1967), 37–52. https://doi.org/10.1007/BF02395039.Google Scholar
Nitzan, S. and Olevskii, A., Revisiting Landau’s density theorems for Paley-Wiener spaces . C. R. Acad. Sci. Paris 350(2012), no. 9–10, 509–512. https://doi.org/10.1016/j.crma.2012.05.003.Google Scholar
Seip, K., On the connection between exponential bases and certain related sequences in L 2(-𝜋, 𝜋) . J. Funct. Anal. 130(1995), no. 1, 131–160. https://doi.org/10.1006/jfan.1995.1066.Google Scholar
Young, R. M., An introduction to nonharmonic Fourier series, Pure and Applied Mathematics, 93, Academic Press, New York, 1980.Google Scholar