Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-20T17:28:01.006Z Has data issue: false hasContentIssue false
  • English
  • Français

A Theorem on the Denseness of Orbits in Metric Spaces

Published online by Cambridge University Press:  20 November 2018

Abraham Boyarsky  and
Manny Scarowksy
Abraham Boyarsky
Affiliation:
Department of Mathematics, Sir George Williams Campus, Concordia University Montreal, Canada
Manny Scarowksy
Affiliation:
Department of Mathematics, Sir George Williams Campus, Concordia University Montreal, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let τ be a transformation from a compact metric space X into itself. Conditions are presented which ensure that there exists an orbit 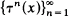which is dense in X. An example is given.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 23 , Issue 4 , 01 December 1980 , pp. 469 - 471
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Boyarsky, A. and Scarowsky, M., On a class of transformations which have unique absolutely continuous invariant measures, Trans. Amer. Math. Soc. 255, (1979) 243-262.Google Scholar
2. Avez, M. A., Propriétés ergodiques des endomorphismes dilatants des variété compactes, C.R. Acad. Se. Paris, Série A, t. 266, (1968) 610-612.Google Scholar
3. Krzyzewski, K. and Szlenk, W., On invariant measures for expanding differentiable mappings, Studia Mathematica, T. XXXIII, (1962) 83-92.Google Scholar
4. Guckenheimer, J., Oster, G., and Jpaktchi, A., The dynamics of denisty dependent population models, J. Math. Biol., 4, (1977) 101-147.Google Scholar
5. Marotto, F. R., Snap-back repellers imply chaos in Rn, Jour. Math. Anal, and Appl. 63, (1978) 199-223.Google Scholar
6. Walters, P., Invariant measures and equilibrium states for some mappings which expand distances, Trans. Amer. Math. Soc. 236, (1978) 121-153.Google Scholar
7. Lasota, A. and Yorke, J. A., On the existence of invariant measures for piecewise monotonie transformations, Trans. Amer. Math. Soc. 186, (1973) 481-488.Google Scholar