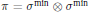Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
MORIWAKI, MASAYASU
2008.
MULTIPLICITY-FREE DECOMPOSITIONS OF THE MINIMAL REPRESENTATION OF THE INDEFINITE ORTHOGONAL GROUP.
International Journal of Mathematics,
Vol. 19,
Issue. 10,
p.
1187.
Möllers, Jan
and
Schwarz, Benjamin
2014.
Branching laws for small unitary representations ofGL(n, ℂ).
International Journal of Mathematics,
Vol. 25,
Issue. 06,
p.
1450052.