Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T08:36:11.162Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur les singularités de la fonction croissance d’une variété non simplement connexe

Published online by Cambridge University Press:  20 November 2018

Lucia Ardizzone ,
Renata Grimaldi  and
Pierre Pansu
Lucia Ardizzone
Affiliation:
Dipartimento di Matematica ed Appl. Fac. di Ingegneria, Viale delle Scienze, 90128 Palermo, Italie, courriel: [email protected]@dipmat.math.unipa.it
Renata Grimaldi
Affiliation:
Dipartimento di Matematica ed Appl. Fac. di Ingegneria, Viale delle Scienze, 90128 Palermo, Italie, courriel: [email protected]@dipmat.math.unipa.it
Pierre Pansu
Affiliation:
Université Paris-Sud, Département de Mathématiques, Bat. 425, 91405 Orsay Cedex, France, courriel: [email protected]
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Si 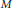$M$ est une variété de dimension $n$, compacte non simplement connexe, on caractérise les métriques riemanniennes sur 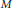$M$ dont la fonction croissance a exactement deux singularités.

Keywords

53B20fonction croissancesingularitésfonction de MorseCutlocus
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 2 , 01 June 2002 , pp. 161 - 167
Copyright
Copyright © Canadian Mathematical Society 2002

References

Références

[1] Akbulut, S. et Kirby, R., An exotic involution of S4. Topology 18 (1979), 18–1979.Google Scholar
[2] Gallot, S., Hulin, D. et Lafontaine, J., Riemannian Geometry. Universitext, Springer-Verlag, Berlin, 1993.Google Scholar
[3] Grimaldi, R. et Pansu, P., Sur la croissance du volume dans une classe conforme. J. Math. Pures Appl. 71 (1992), 71–1992.Google Scholar
[4] Grimaldi, R. et Pansu, P., Sur la régularité de la fonction croissance d’une variété riemannienne. Geom. Dedicata (3) 50 (1994), 50–1994.Google Scholar
[5] Grimaldi, R. et Pansu, P., Sur le degré de différentiabilité de la fonction croissance en dimension deux. Boll. Un. Mat. Ital. B (7) suppl. (2) 11 (1997), 11–1997.Google Scholar
[6] Grimaldi, R. et Pansu, P., Nombre de singularités de la fonction croissance en dimension 2. Bull. Soc. Math. Belg. 8 (2001), 8–2001.Google Scholar
[7] Hirsch, M. W. et Milnor, J., Some curious involutions of spheres. Bull. Amer. Math. Soc. 70 (1964), 70–1964.Google Scholar
[8] Hirzebruch, F. et Mayer, K. H., O(n)-Mannigfaltigkeiten, exotische Sphären und Singularitäten. Lecture Notes in Math. 57, Springer-Verlag, Berlin, 1968.Google Scholar
[9] Livesay, G. R., Fixed point free involutions on the 3-sphere. Ann. of Math. 72 (1960), 72–1960.Google Scholar
[10] de Medrano, S. Lopez, Involutions on manifolds. Ergebnisse der Math. 59, Springer-Verlag, Berlin, 1971.Google Scholar
[11] Mayer, K. H., Fixpunktfreie Involutionen von 7-Sphären. Math. Ann. 185 (1970), 185–1970.Google Scholar