Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T00:50:29.663Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur les invariants d'Iwasawa des tours cyclotomiques

Published online by Cambridge University Press:  20 November 2018

Jean-François Jaulent  and
Christian Maire
Jean-François Jaulent
Affiliation:
Université Bordeaux 1, Institut de Mathématiques, 351, cours de la Libération, F-33405 Talence Cedex, France, e-mail: [email protected]
Christian Maire
Affiliation:
Université Bordeaux 1, Institut de Mathématiques, 351, cours de la Libération, F-33405 Talence Cedex, France et DMA, Ecole Poly. Fédérale de Lausanne, 1015 Lausanne, Suisse, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We carry out the computation of the Iwasawa invariants 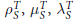$\rho _{S}^{T},\,\mu _{S}^{T},\,\lambda _{S}^{T}$ associated to abelian 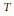$T$-ramified 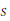$S$-decomposed 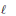$\ell$-extensions over the finite steps 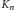${{K}_{n}}$ of the cyclotomic 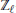${{\mathbb{Z}}_{\ell }}$ -extension 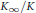${{K}_{\infty }}/K$ of a number field of CM-type.

Résumé

Résumé

Nous déterminons explicitement les paramétres d'Iwasawa 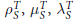$\rho _{S}^{T},\,\mu _{S}^{T},\,\lambda _{S}^{T}$ des 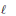$\ell$-groupes de 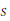$S$-classes 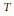$T$-infinitésimales $\text{Cl}_{S}^{T}\left( {{K}_{n}} \right)$ attachés aux étages finis de la 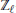${{\mathbb{Z}}_{\ell }}$-extension cyclotomique 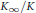${{K}_{\infty }}/K$ d'un corps de nombres à conjugaison complexe.

Keywords

11R2311R37
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 2 , 01 June 2003 , pp. 178 - 190
Copyright
Copyright © Canadian Mathematical Society 2003

References

Références

[1] Gras, G., Théorèmes de réflexion. J. Théor. Nombres Bordeaux 10 (1998), 399–499.Google Scholar
[2] Jaulent, J.-F., L'arithmétique des l-extensions (Thèse d'Etat). Publ. Math. Fac. Sci. Besançon Théor. Nombres 1985–86, (1986).Google Scholar
[3] Jaulent, J.-F., La Théorie de Kummer et le K2 des corps de nombres. J. Théor. Nombres Bordeaux 2 (1990), 377–411.Google Scholar
[4] Jaulent, J.-F., Généralisation d'un théorème d'Iwasawa. Prépublication.Google Scholar
[5] Serre, J.-P., Classes des corps cyclotomiques (d'après Iwasawa). Séminaire Bourbaki, exp. 174 (1958).Google Scholar
[6] Washington, L. C., Introduction to cyclotomic fields. Graduate Texts in Math. 83, Springer-Verlag 1982.Google Scholar