No CrossRef data available.
Article contents
Sur les Anneaux Partiellement Ordonnés
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Un anneau partiellement ordonné A est un anneau sur lequel est définie une relation d'ordre partiel telle que:
1. a≥b entraîne a+c≥+c pour tout c∈A.
2. a≥o et b≥o entraînent ab≥o.
Si la relation d'ordre est une relation d1 ordre total, l'anneau A est dit un anneau totalement ordonné.
Il est bien connu (Théorème d'artin-Schreier [l]) que, pour qu'un corps commutatif K puisse être totalement ordonné, il faut et il suffit que la relation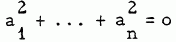 
entraîne a1=…=an=o. Ce théorème a été généralisé par T. Szele [4] qui a montré que, pour qu'un corps quelconque K puisse être totalement ordonné, il faut et il suffit que le demi-groupe additif et multiplicatif S, engendré par les éléments de K qui sont des carrés non nuls, ne contienne pas I'élément zéro de K. Ce résultat a été étendu au cas d1 un anneau d'intégrité par R.E. Johnson [2] de la manière suivante.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1962
References
1.
Artin, E. und Schreier, O., Algebraische Konstruction realler Kőrper, Abh. Math. Sem. Univ. Hambourg, 5(1926), 85-89.10.1007/BF02952512Google Scholar
2.
Johnson, R. E., On ordered domains of integrity, Proc. Amer. Math. Soc, 3(1952), 414-416.10.1090/S0002-9939-1952-0047018-9Google Scholar
3.
McCoy, N. H., Prime ideals in general rings, Amer. J. Math., 71 (1949), 823-833.10.2307/2372366Google Scholar
4.
Szele, T., On ordered skew fields, Proc. Amer. Math. Soc. 3 (1952), 410-413.10.1090/S0002-9939-1952-0047017-7Google Scholar
5.
Thierrin, G., Sur les idéaux compl?terrent premiers d'un anneau quelconque, Bull. Acad. Royale de Belgique, 43 (1957), 124-132.Google Scholar
You have
Access