Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T05:57:15.819Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure in Sets with Logarithmic Doubling

Published online by Cambridge University Press:  20 November 2018

T. Sanders
T. Sanders*
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Cambridge CB3 0WB, UK e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

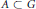Suppose that $G$ is an abelian group, $A\,\subset \,G$ is finite with 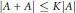$\left| A\,+\,A \right|\,\le \,K\left| A \right|$ and 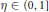$\eta \,\in \,(0,\,1]$ is a parameter. Our main result is that there is a set 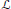$L$ such that

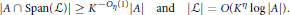$$\left| A\,\cap \,\text{Span}\left( L \right) \right|\ge {{K}^{-{{O}_{n}}\left( 1 \right)}}\left| A \right|\,\,\,\,\text{and}\,\,\,\,\,\left| L \right|=O\left( {{K}^{n}}\log \left| A \right| \right).$$

We include an application of this result to a generalisation of the Roth-Meshulam theorem due to Liu and Spencer

Keywords

11B25Fourier analysisFreiman's theoremcapset problem
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 2 , 01 June 2013 , pp. 412 - 423
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Balog, A. and E. Szemerédi, A statistical theorem of set addition. Combinatorica 14(1994), no. 3, 263–268. http://dx.doi.org/10.1007/BF01212974 Google Scholar
[2] Chang, M.-C., A polynomial bound in Fre˘ıman's theorem. Duke Math. J. 113(2002), no. 3, 399–419. http://dx.doi.org/10.1215/S0012-7094-02-11331-3 Google Scholar
[3] Croot, E. S. and Lev, V. F., Open problems in additive combinatorics. In: Additive Combinatorics. CRM Proc. Lecture Notes 43. American Mathematical Societh, Providence, RI, 2007, pp. 207–233. Google Scholar
[4] Freĭman, G. A., Foundations of a Structural Theory of Set Addition. Translations of Mathematical Monographs 37. American Mathematical Society, Providence, RI, 1973.Google Scholar
[5] Gowers, W. T., A new proof of Szemerédi's theorem for arithmetic progressions of length four. Geom. Funct. Anal. 8(1998), no. 3, 529–551. http://dx.doi.org/10.1007/s000390050065 Google Scholar
[6] Green, B. J. and Ruzsa, I. Z., Fre˘ıman's theorem in an arbitrary abelian group. J. Lond. Math. Soc. 75(2007), no. 1, 163–175. http://dx.doi.org/10.1112/jlms/jdl021 Google Scholar
[7] Green, B. J., Finite field models in additive combinatorics. In: Surveys in Combinatorics 2005. London Math. Soc. Lecture Note Ser. 327. Cambridge Univ. Press, Cambridge, 2005, pp. 1–27. Google Scholar
[8] Löpez, J. M. and Ross, K. A., Sidon Sets. Lecture Notes in Pure and Applied Mathematics, 13. Marcel Dekker, New York, 1975.Google Scholar
[9] Liu, Y.-R. and Spencer, C. V., A generalization of Meshulam's theorem on subsets of finite abelian groups with no 3-term arithmetic progression. Des. Codes Cryptogr. 52(2009), no. 1, 83–91. http://dx.doi.org/10.1007/s10623-009-9268-0 Google Scholar
[10] Liu, Y.-R., Spencer, C. V., and Zhao, X., A generalization of Meshulam's theorem on subsets of finite abelian groups with no 3-term arithmetic progression. II. European J. Combin. 32(2011), no. 2, 258–264. http://dx.doi.org/10.1016/j.ejc.2010.09.008 Google Scholar
[11] Meshulam, R.. On subsets of finite abelian groups with no 3-term arithmetic progressions. J. Combin. Theory Ser. A 71(1995), no. 1, 168–172. http://dx.doi.org/10.1016/0097-3165(95)90024-1 Google Scholar
[12] Roth, K. F., On certain sets of integers. J. London Math. Soc. 28(1953), 104–109. http://dx.doi.org/10.1112/jlms/s1-28.1.104 Google Scholar
[13] Rudin, W., Fourier Analysis on Groups. Reprint of the 1962 original. JohnWiley & Sons, New York, 1990.Google Scholar
[14] Ruzsa, I. Z., Solving a linear equation in a set of integers. I. Acta Arith. 65(1993), no. 3, 259–282. Google Scholar
[15] Ruzsa, I. Z., Generalized arithmetical progressions and sumsets. Acta Math. Hungar. 65(1994), no. 4, 379–388. http://dx.doi.org/10.1007/BF01876039 Google Scholar
[16] Sanders, T., On a non-abelian Balog–Szemerédi-type lemma. J. Aust. Math. Soc. 89(2010), no.1, 127–132. Google Scholar
[17] Schoen, T., Near optimal bounds in Freıman's theorem. Preprint, 2010.Google Scholar
[18] Shkredov, I. D., On sets of large trigonometric sums. Izv. Ross. Akad. Nauk Ser. Mat. 72(2008), no. 1, 161–182. Google Scholar
[19] Shkredov, I. D., On sets with small doubling. Mat. Zametki 84(2008), no. 6, 927–947. Google Scholar
[20] Szemerédi, E., Integer sets containing no arithmetic progressions. Acta Math. Hungar. 56(1990), no. 1-2, 155–158. http://dx.doi.org/10.1007/BF01903717 Google Scholar
[21] Tao, T. C., Structure and Randomness. Pages from Year One of a Mathematical Blog.. American Mathematical Society, Providence, RI, 2008.Google Scholar
[22] Tao, T. C. and Vu, H. V., Additive Combinatorics. Cambridge Studies in Advanced Mathematics 105. Cambridge University Press, Cambridge, 2006.Google Scholar