Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T07:31:49.353Z Has data issue: false hasContentIssue false
  • English
  • Français

Strongly 0-dimensional Modules

Published online by Cambridge University Press:  20 November 2018

Kürşat Hakan Oral ,
Neslihan Ayşen Özkirişci  and
Ünsal Tekir
Kürşat Hakan Oral
Affiliation:
Yildiz TechnicalUniversity, Department ofMathematics, Davutpasa Campus, Esenler, 34210, Istanbul, Turkey e-mail: [email protected]@yildiz.edu.tr
Neslihan Ayşen Özkirişci
Affiliation:
Marmara University, Department of Mathematics, 34722, Ziverbey, Kadıköy, Istanbul, Turkey e-mail: [email protected]
Ünsal Tekir
Affiliation:
Yildiz TechnicalUniversity, Department ofMathematics, Davutpasa Campus, Esenler, 34210, Istanbul, Turkey e-mail: [email protected]@yildiz.edu.tr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a multiplication module, prime submodules have the following property: if a prime submodule contains a finite intersection of submodules, then one of the submodules is contained in the prime submodule. In this paper, we generalize this property to infinite intersection of submodules and call such prime submodules strongly prime submodules. A multiplication module in which every prime submodule is strongly prime will be called a strongly 0-dimensional module. It is also an extension of strongly 0-dimensional rings. After this we investigate properties of strongly 0-dimensional modules and give relations of von Neumann regular modules, 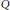$Q$-modules and strongly 0-dimensional modules.

Keywords

13C9916D10Strongly 0-dimensional ringsQ-moduleVon Neumann regular module
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 1 , 14 March 2014 , pp. 159 - 165
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Ali, M. M., Idempotent and nilpotent submodules of multiplication modules. Comm. Algebra 36 (2008), no. 12, 4620–4642. http://dx.doi.org/10.1080/00927870802186805 Google Scholar
[2] El-Bast, Z. A. and Smith, P. F., Multiplication modules. Comm. Algebra 16 (1988), no. 4, 755–779. http://dx.doi.org/10.1080/00927878808823601 Google Scholar
[3] Jayaram, C. and Tekir, Ü., Q-modules. Turkish J. Math. 33 (2009), no. 3, 215–225.Google Scholar
[4] Jayaram, C., Oral, K. H., and Tekir, Ü., Strongly 0-dimensional rings. Comm. Algebra, to appear.Google Scholar
[5] Kash, F., Modules and rings. London Mathematical Society Monographs, 17, Academic Press, London-New York, 1982.Google Scholar
[6] Lu, C.-P., Prime submodules of modules. Comment. Math. Univ. St. Paul 33 (1984), no. 1, 61–69.Google Scholar
[7] Lu, C.-P., Spectra of modules. Comm. Algebra 23 (1995), no. 10, 3741–3752. http://dx.doi.org/10.1080/00927879508825430 Google Scholar
[8] Moore, M. E. and Smith, S. J., Prime and radical submodules of modules over commutative rings. Comm. Algebra 30 (2002), no. 10, 5037–5064. http://dx.doi.org/10.1081/AGB-120014684 Google Scholar
[9] Northcott, D. G., Lessons on rings, modules and multiplicities. Cambridge University Press, London, 1968.Google Scholar