Hostname: page-component-f554764f5-nt87m Total loading time: 0 Render date: 2025-04-11T17:49:18.261Z Has data issue: false hasContentIssue false
  • English
  • Français

Star-Shapedness and K-Orbits in Complex Semisimple Lie Algebras

Published online by Cambridge University Press:  20 November 2018

Wai-Shun Cheung  and
Tin-Yau Tam
Wai-Shun Cheung
Affiliation:
Department of Mathematics and Statistics, Auburn University, AL 36849–5310, U.S.A.e-mail: [email protected]@auburn.edu
Tin-Yau Tam
Affiliation:
Department of Mathematics and Statistics, Auburn University, AL 36849–5310, U.S.A.e-mail: [email protected]@auburn.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

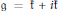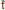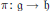Given a complex semisimple Lie algebra $\mathfrak{g}=\mathfrak{k}+i\mathfrak{k}$ ($\mathfrak{t}$ is a compact real form of $\mathfrak{g}$), let $\text{ }\pi \text{ }\text{:}\mathfrak{g}\to \mathfrak{h}$ be the orthogonal projection (with respect to the Killing form) onto the Cartan subalgebra 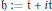$\mathfrak{h}:=\mathfrak{t}\text{+}i\mathfrak{t}$, where $\mathfrak{t}$ is a maximal abelian subalgebra of 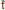$\mathfrak{k}$. 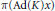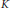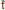Given $x\,\in \,\mathfrak{g}$, we consider $\text{ }\!\!\pi\!\!\text{ (Ad(}K\text{)}x)$, where $K$ is the analytic subgroup $G$ corresponding to $\mathfrak{k}$, and show that it is star-shaped. The result extends a result of Tsing. We also consider the generalized numerical range 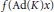$f(\text{Ad(}K\text{)}x)$, where 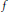$f$ is a linear functional on $\mathfrak{g}$. We establish the star-shapedness of 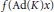$f(\text{Ad(}K\text{)}x)$ for simple Lie algebras of type $B$.

Keywords

22E1017B20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 1 , 01 March 2011 , pp. 44 - 55
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Au-Yeung, Y. H. and Sing, F. Y., A remark on the generalized numerical range of a normal matrix. Glasgow Math. J. 18(1977), no. 2, 179–180. doi:10.1017/S0017089500003244Google Scholar
[2] Au-Yeung, Y. H. and Tsing, N. K., A conjecture of Marcus on the generalized numerical range. Linear and Multilinear Algebra 14(1983), no. 3, 235–239. doi:10.1080/03081088308817560Google Scholar
[3] Bourbaki, N., Lie groups and Lie algebras. Chapters 1-3, Springer-Verlag, New York, 1971.Google Scholar
[4] Cheung, W.-S. and Tsing, N.-K., The C-numerical range of matrices is star-shaped. Linear and Multilinear Algebra 41(1996), no. 3, 245–250. doi:10.1080/03081089608818479Google Scholar
[5] Đoković, D. Z. and Tam, T. Y., Some questions about semisimple Lie groups originating in matrix theory. Canad. Math. Bull. 46(2003), no. 3, 332–343.Google Scholar
[6] Helgason, S., Differential geometry, Lie groups and symmetric spaces. Pure and Applied Mathematics, 80, Academic Press, New York-London, 1978.Google Scholar
[7] Horn, A., Doubly stochastic matrices and the diagonal of a rotation matrix. Amer. J. Math. 76(1954), 620–630. doi:10.2307/2372705Google Scholar
[8] Horn, R. A. and Johnson, C. R., Matrix analysis. Cambridge University Press, Cambridge, 1985.Google Scholar
[9] Horn, R. A. and Johnson, C. R., Topics in matrix analysis. Cambridge University Press, Cambridge, 1991.Google Scholar
[10] Humphreys, J. E., Introduction to Lie algebras and representation theory. Graduate Texts in Mathematics, 9, Springer-Verlag, New York-Berlin, 1972.Google Scholar
[11] Kostant, B., On convexity, the Weyl group and Iwasawa decomposition. Ann. Sci. École Norm. Sup. 6(1973), 413–455.Google Scholar
[12] Knapp, A. W., Lie groups beyond an introduction. Progress in Mathematics, 140, Birkhäuser Boston, Boston, MA, 1996.Google Scholar
[13] Marhall, A. W. and Olkin, I., Inequalities: theory of majorizations and its applications. Mathematics in Science and Engineering, 143, Academic Press, New York-London, 1979.Google Scholar
[14] Schur, I., Über eine Klasse von Mittelbildungen mit Anwendungen auf die Determinantentheorie. Sitzungsber. Berl. Math. Ges. 22(1923), 9–20.Google Scholar
[15] Tam, T. Y., On the shape of numerical ranges associated with Lie groups. Taiwanese J. Math. 5(2001), no. 3, 497–506.Google Scholar
[16] Tam, T.-Y. and Cheung, W.-S., The K-orbit of a normal element in a complex semisimple Lie algebra. Pacific J. Math. 238(2008), no. 2, 387–398. doi:10.2140/pjm.2008.238.387Google Scholar
[17] Tsing, N. K., On the shape of the generalized numerical ranges. Linear and Multilinear Algebra 10(1981), no. 3, 173–182. doi:10.1080/03081088108817410Google Scholar
[18] Warner, F. W., Foundations of differentiable manifolds and Lie groups. Graduate Texts in Mathematics, 94, Springer-Verlag, New York-Berlin, 1983.Google Scholar