Article contents
Square-Reduced Residue Systems (Mod r) and Related Arithmetical Functions
Published online by Cambridge University Press: 20 November 2018
Abstract
We define a square-reduced residue system (mod r) as the set of integers a (mod r) such that the greatest common divisor of a and r, denoted by (a, r), is a perfect square ≥ 1 and contained in a residue system (mod r). This leads to a Class-division of integers (mod r) based on the 'square-free' divisors of r. The number of elements in a square-reduced residue system (mod r) is denoted by b(r). It is shown that
(1)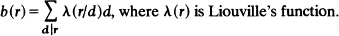
(2)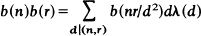
In view of (2), b(r) is said to be 'specially multiplicative'. The exponential sum associated with a square-reduced residue system (mod r) is defined by
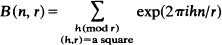
where the summation is over a square-reduced residue system (mod r).
B(n, r) belongs to a new class of multiplicative functions known as 'Quasi-symmetric functions' and
(3)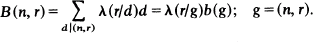
As an application, the sum  is considered in terms of the Cauchy-composition of even functions (mod r). It is found to be multiplicative in r. The evaluation of the above sum gives an identity involving Pillai's arithmetic function
is considered in terms of the Cauchy-composition of even functions (mod r). It is found to be multiplicative in r. The evaluation of the above sum gives an identity involving Pillai's arithmetic function
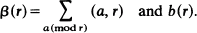
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1979
References
- 5
- Cited by


