Springer's Weyl Group Representation via Localization

Abstract

Let 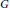$G$ denote a reductive algebraic group over 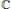$\mathbb{C}$ and $x$ a nilpotent element of its Lie algebra $\mathfrak{g}$. The Springer variety 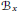${{B}_{x}}$ is the closed subvariety of the flag variety 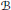$B$ of 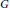$G$ parameterizing the Borel subalgebras of $\mathfrak{g}$ containing $x$. It has the remarkable property that the Weyl group 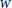$W$ of 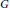$G$ admits a representation on the cohomology of 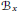${{B}_{x}}$ even though 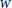$W$ rarely acts on 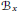${{B}_{x}}$ itself. Well-known constructions of this action due to Springer and others use technical machinery from algebraic geometry. The purpose of this note is to describe an elementary approach that gives this action when $x$ is what we call parabolic-surjective. The idea is to use localization to construct an action of 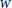$W$ on the equivariant cohomology algebra 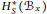$H_{s}^{*}({{B}_{x}})$, where $S$ is a certain algebraic subtorus of 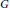$G$. This action descends to 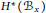${{H}^{*}}({{B}_{x}})$ via the forgetful map and gives the desired representation. The parabolic-surjective case includes all nilpotents of type $A$ and, more generally, all nilpotents for which it is known that 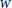$W$ acts on 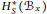$H_{s}^{*}({{B}_{x}})$ for some torus $S$. Our result is deduced from a general theorem describing when a group action on the cohomology of the ûxed point set of a torus action on a space lifts to the full cohomology algebra of the space.