Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T07:25:38.090Z Has data issue: false hasContentIssue false
  • English
  • Français

SP Transform and Uniform Convergence of Laurent and Power Series

Published online by Cambridge University Press:  20 November 2018

S.A. Settu
S.A. Settu*
Affiliation:
Ramanujan Institute University of Madras Madras-600 005 India
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If the Laurent series

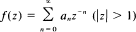
is transformed to

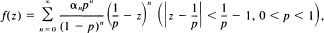
it is shown that convergence of the former at z = 1 implies the uniform convergence of the latter on a symmetric arc of |z - 1/P| = 1/P - 1 not containing z = 1 and that the uniform convergence of the former over a symmetric arc of |z| = 1 containing z = 1 implies uniform convergence of the latter on the entire circle |z — 1/P| = 1/P — 1.

Keywords

Primary 30B30Secondary 40G99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 30 , Issue 1 , 01 March 1987 , pp. 114 - 123
Copyright
Copyright © Canadian Mathematical Society 01

References

1. Hardy, G.H., Divergent Series, Oxford, 1949.Google Scholar
2. Jakimovski, A. and W., Meyer-König, Uniform convergence of power series expansions on the boundary, J. reine angew. Math., 318 (1980), pp. 126–136.Google Scholar
3. Meyer-König, W., Vntersuchungen über einige verwandte Limitierungsverfahren, Math. Zeit., 52 (1949), pp. 257–304.Google Scholar
4. Vermes, P., Series to series transformations and analytic continuation by matrix methods, Amer. J. Math. 71 (1949), pp. 541–562.Google Scholar
5. Zeller, K. and Beekmann, W., Théorie der Limitierungsverfahren, 2, Aufl., Berlin-Heidelberg-New York, 1970.Google Scholar