Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T12:26:50.703Z Has data issue: false hasContentIssue false
  • English
  • Français

Sommes de la Forme

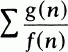
Published online by Cambridge University Press:  20 November 2018

Armel Mercier
Armel Mercier*
Affiliation:
Université du Québec à Chicoutimi, Chicoutimi (Québec)G7H 2B1
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Dans [8], nous avons étudié l'ordre de grandeur des sommes de la forme 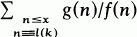, pour 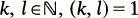ou k, où g(n) et f(n) appartiennent respectivement à une classe de fonctions multiplicatives et additives.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 24 , Issue 3 , 01 September 1981 , pp. 299 - 307
Copyright
Copyright © Canadian Mathematical Society 1981

References

Bibliographie

1. Chandrasekharan, K., Introduction to analytic number theory, Springer-Verlag, 1968.Google Scholar
2. De Koninck, J. M., On a class of arithmetical functions, Duke Math. J.. 39 (1972), 807-818.Google Scholar
3. De Koninck, J. M. et Mercier, A., Remarque sur un article de T. M. Apostol, Cand. Math. Bull. Vol. 20 (1), 1977, 77-78.Google Scholar
4. Duncan, R. L., A class of additive arithmetical functions, Amer. Math. Month.. 69 (1962), 34-36.Google Scholar
5. Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers, Oxford University Press, London, 1968.Google Scholar
6. Mercier, A., Sommes de fonctions addiatives restreintes à une classe de congruence, Canad. Math. Bull., Vol. 22 (1), 1979, 59-73.Google Scholar
7. Mercier, A., Identité pour, Canad. Math. Bull., Vol. 22 (3), 1979, 317-325. n-I(k)Google Scholar
8. Mercier, A., On a class of distributive functions (soumis pour publication).Google Scholar
9. Selberg, A., Note on a paper by L. G. Sathe, J. Indian Math. Soc. 18 (1962), 83-87.Google Scholar