Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-22T17:18:57.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Properties of Hankel Convolution Operators

Published online by Cambridge University Press:  20 November 2018

J. J. Betancor  and
I. Marrero
J. J. Betancor
Affiliation:
Departamento de Anâlisis Matematico Universidad de La Laguna 38271 La Laguna (Tenerife) Canary Islands Spain
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 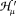be the Zemanian space of Hankel transformable generalized functions and let 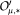be the space of Hankel convolution operators for 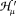. This 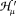is the dual of a subspace 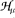of 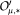for which 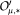is also the space of Hankel convolutors. In this paper the elements of 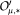are characterized as those in 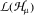and in 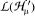that commute with Hankel translations. Moreover, necessary and sufficient conditions on the generalized Hankel transform 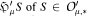are established in order that every 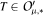such that 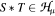in .

Keywords

46F12generalized functionsHankel transformationHankel translationHankel convolution
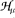Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 36 , Issue 4 , 01 December 1993 , pp. 398 - 406
Copyright
Copyright © Canadian Mathematical Society 1993

References

1. Kelley, J. L., General Topology, D. van Nostrand, Princeton, New Jersey, 1968.Google Scholar
2. Betancor, J. J. and Marrero, I., Structure and convergence in certain spaces of distributions and the generalized Hankel convolution, Math. Japon, to appear.Google Scholar
3. Marrero, I. and Betancor, J. J., Hankel convolution of generalized functions, 1992, preprint.Google Scholar
4. Sznajder, S. and Zielezny, Z., On some properties of convolution operators in K1′ and S′, J. Math. Anal. Appl. 65(1978), 543–554.Google Scholar
5. Zemanian, A. H., Generalized Integral Transformations, Interscience, New York, 1968.Google Scholar