Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hirzallah, Omar
and
Kittaneh, Fuad
2000.
Matrix Young inequalities for the Hilbert–Schmidt norm.
Linear Algebra and its Applications,
Vol. 308,
Issue. 1-3,
p.
77.
Hirzallah, Omar
and
Kittaneh, Fuad
2002.
Norm inequalities for weighted power means of operators.
Linear Algebra and its Applications,
Vol. 341,
Issue. 1-3,
p.
181.
Hirzallah, Omar
2005.
Inequalities for sums and products of operators.
Linear Algebra and its Applications,
Vol. 407,
Issue. ,
p.
32.
Jocić, Danko R.
2005.
Cauchy–Schwarz norm inequalities for weak∗-integrals of operator valued functions.
Journal of Functional Analysis,
Vol. 218,
Issue. 2,
p.
318.
Hirzallah, Omar
and
Kittaneh, Fuad
2007.
Inequalities for sums and direct sums of Hilbert space operators.
Linear Algebra and its Applications,
Vol. 424,
Issue. 1,
p.
71.
Shebrawi, Khalid
and
Albadawi, Hussien
2010.
Norm inequalities for the absolute value of Hilbert space operators.
Linear and Multilinear Algebra,
Vol. 58,
Issue. 4,
p.
453.
Albadawi, Hussien
2012.
Hölder-type inequalities involving unitarily invariant norms.
Positivity,
Vol. 16,
Issue. 2,
p.
255.
Moslehian, Mohammad Sal
Matharu, Jagjit Singh
and
Aujla, Jaspal Singh
2012.
Non-commutative Callebaut inequality.
Linear Algebra and its Applications,
Vol. 436,
Issue. 9,
p.
3347.
Turkmen, Ramazan
Paksoy, Vehbi E.
and
Zhang, Fuzhen
2012.
Some inequalities of majorization type.
Linear Algebra and its Applications,
Vol. 437,
Issue. 6,
p.
1305.
Audeh, Wasim
and
Kittaneh, Fuad
2012.
Singular value inequalities for compact operators.
Linear Algebra and its Applications,
Vol. 437,
Issue. 10,
p.
2516.
Bekjan, Turdebek N.
and
Ospanov, Myrzagali N.
2017.
Holder-type inequalities of measurable operators.
Positivity,
Vol. 21,
Issue. 1,
p.
113.
Dodds, P. G.
Dodds, T. K.
Sukochev, F. A.
and
Zanin, D.
2020.
Arithmetic–Geometric Mean and Related Submajorisation and Norm Inequalities for $$\tau $$-Measurable operators: Part I.
Integral Equations and Operator Theory,
Vol. 92,
Issue. 3,
Dodds, P.G.
Dodds, T.K.
Sukochev, F.A.
and
Zanin, D.
2020.
Logarithmic submajorization, uniform majorization and Hölder type inequalities for τ-measurable operators.
Indagationes Mathematicae,
Vol. 31,
Issue. 5,
p.
809.
Kittaneh, Fuad
and
Zamani, Ali
2023.
Bounds for A-numerical radius based on an extension of A-Buzano inequality.
Journal of Computational and Applied Mathematics,
Vol. 426,
Issue. ,
p.
115070.
Bikchentaev, Airat M.
Kittaneh, Fuad
Moslehian, Mohammad Sal
and
Seo, Yuki
2024.
Trace Inequalities.
p.
111.
Al-Natoor, Ahmad
Hirzallah, Omar
and
Kittaneh, Fuad
2024.
Singular value and norm inequalities involving the numerical radii of matrices.
Annals of Functional Analysis,
Vol. 15,
Issue. 1,
Bikchentaev, Airat M.
Kittaneh, Fuad
Moslehian, Mohammad Sal
and
Seo, Yuki
2024.
Trace Inequalities.
p.
19.
Audeh, Wasim
Al-Boustanji, Anwar
Al-Labadi, Manal
and
Al-Naimi, Raja’a
2024.
Singular value inequalities of matrices via increasing functions.
Journal of Inequalities and Applications,
Vol. 2024,
Issue. 1,
Aici, Soumia
Frakis, Abdelkader
and
Kittaneh, Fuad
2025.
On p-numerical radius inequalities for sums and products of operators.
The Journal of Analysis,
Vol. 33,
Issue. 2,
p.
673.
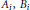 ${{A}_{i}},\,{{B}_{i}}$ and
${{A}_{i}},\,{{B}_{i}}$ and 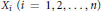 ${{X}_{i}}\,(i\,=\,1,\,2,\ldots ,\,n)$ be operators on a separable Hilbert space. It is shown that if
${{X}_{i}}\,(i\,=\,1,\,2,\ldots ,\,n)$ be operators on a separable Hilbert space. It is shown that if 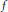 $f$ and
$f$ and  $g$ are nonnegative continuous functions on
$g$ are nonnegative continuous functions on  $\left[ 0,\infty \right)$ which satisfy the relation
$\left[ 0,\infty \right)$ which satisfy the relation 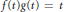 $f\,(t)g(t)\,=\,t$ for all
$f\,(t)g(t)\,=\,t$ for all  $t$ in
$t$ in  $\left[ 0,\infty \right)$, then
$\left[ 0,\infty \right)$, then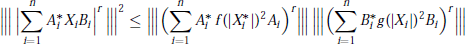 $${{\left\| \left| \,{{\left| \sum\limits_{i=1}^{n}{A_{i}^{*}{{X}_{i}}{{B}_{i}}} \right|}^{r}} \right| \right\|}^{2}}\,\le \,\left\| \left| {{\left( \sum\limits_{i=1}^{n}{A_{i}^{*}f{{(\left| X_{i}^{*} \right|)}^{2}}{{A}_{i}}} \right)}^{r}} \right| \right\|\,\,\left\| \left| {{\left( \sum\limits_{i=1}^{n}{B_{i}^{*}g{{(\left| {{X}_{i}} \right|)}^{2}}\,{{B}_{i}}} \right)}^{r}} \right| \right\|$$
$${{\left\| \left| \,{{\left| \sum\limits_{i=1}^{n}{A_{i}^{*}{{X}_{i}}{{B}_{i}}} \right|}^{r}} \right| \right\|}^{2}}\,\le \,\left\| \left| {{\left( \sum\limits_{i=1}^{n}{A_{i}^{*}f{{(\left| X_{i}^{*} \right|)}^{2}}{{A}_{i}}} \right)}^{r}} \right| \right\|\,\,\left\| \left| {{\left( \sum\limits_{i=1}^{n}{B_{i}^{*}g{{(\left| {{X}_{i}} \right|)}^{2}}\,{{B}_{i}}} \right)}^{r}} \right| \right\|$$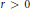 $r\,>\,0$ and for every unitarily invariant norm. This result improves some known Cauchy-Schwarz type inequalities. Norm inequalities related to the arithmetic-geometric mean inequality and the classical Heinz inequalities are also obtained.
$r\,>\,0$ and for every unitarily invariant norm. This result improves some known Cauchy-Schwarz type inequalities. Norm inequalities related to the arithmetic-geometric mean inequality and the classical Heinz inequalities are also obtained.

