Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Imoru, Christopher Olutunde
1987.
Generalizations of Hardy's integral inequality.
Journal of Mathematical Analysis and Applications,
Vol. 122,
Issue. 1,
p.
7.
Mitrinović, D. S.
Pečarić, J. E.
and
Fink, A. M.
1991.
Inequalities Involving Functions and Their Integrals and Derivatives.
p.
143.
Azar, Laith E
2013.
The connection between Hilbert and Hardy inequalities.
Journal of Inequalities and Applications,
Vol. 2013,
Issue. 1,
Tian, Jingfeng
and
Zhou, Yang-Xiu
2013.
Refinements of Hardy-Type Inequalities.
Abstract and Applied Analysis,
Vol. 2013,
Issue. ,
p.
1.
Al-Oushoush, Nizar Kh.
2023.
Half-discrete of Hilbert inequality for three variables.
Afrika Matematika,
Vol. 34,
Issue. 4,


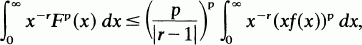
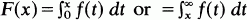 according as r>1 or r < l.
according as r>1 or r < l.