Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T12:39:19.974Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Extensions of the Hausdorff-Young and Paley Theorems

Published online by Cambridge University Press:  20 November 2018

P. S. Bullen
P. S. Bullen*
Affiliation:
University of British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Orthonormal sequences, o.n. s., {ϕn} defined on [0,1] and satisfying

1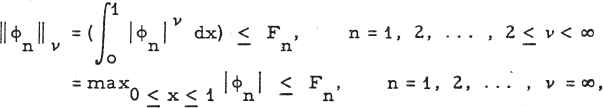

have been studied in [3] and [1]. One of the objects of this paper is to indicate that the methods used to study such o. n. s. can be used for a much wider class, and that, although there seems to be no super theorem to cover all cases, a knowledge of the results and methods of proof in some fairly broad special cases enables one to state and prove theorems for other classes of o. n. s.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 4 , Issue 2 , May 1961 , pp. 123 - 138
Copyright
Copyright © Canadian Mathematical Society 1961

References

1. Bullen, P. S., Properties of the coefficients of orthonormal sequences, Canad. J. Math. Google Scholar
2. Kacmarz, and Steinhaus, , Théorie der Orthogonalreihen, (New York, 1951).Google Scholar
3. Marcinkiewicz, J. and Zygmund, A., Some theorems on orthogonal systems, Fund. Math., 28 (1937), 309-35.Google Scholar
4. Rosskopf, M., Some inequalities for non-uniformly bounded orthonormal polynomials, Trans. Amer. Math. Soc., 36 (1934), 853.Google Scholar
5. Stein, E. and Weiss, G., Interpolation of operators with change of measures, Trans. Amer. Math. Soc., 87 (1958), 159-72.10.1090/S0002-9947-1958-0092943-6Google Scholar
6. Szego, G., Orthogonal Polynomials, Amer. Math. Soc. Coll. Publ. XXIH, 1939.Google Scholar
7. Zygmund, A., Trigonometric Series, Vol. II, 2nd ed., (Cambridge, 1959).Google Scholar