Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T18:01:56.251Z Has data issue: false hasContentIssue false
  • English
  • Français

The Solution to a Problem of Grünbaum

Published online by Cambridge University Press:  20 November 2018

Peter Salamon  and
Paul Erdös
Peter Salamon
Affiliation:
Department of Mathematical Sciences, San Diego State University, San DiegoCA 92182
Paul Erdös
Affiliation:
Hungarian Academy of Sciences, Budapest, Hungary
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The paper characterizes the set of all possible values for the number of lines determined by n points for n sufficiently large. For 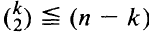the lower bound of Kelly and Moser for the number of lines in a configuration with n — k collinear points is shown to be sharp and it is shown that all values between Mmin(k) and Mmax(k) are assumed with the exception of Mmax — 1 and Mmax — 3. Exact expressions are obtained for the lower end of the continuum of values leading down from 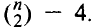In particular, the best value of c = 1 is obtained in Erdös’ previous expression 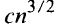for this lower end of the continuum.

Keywords

05-A15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 31 , Issue 2 , 01 June 1988 , pp. 129 - 138
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Beck, J., On the lattice property of the plane and some problems of Dirac, Motzkin and Erdbs in combinatorial geometry, Combinatorica 3 (1983), pp. 281–297.Google Scholar
2. Cordovil, R., Europ. J. Math. 1 (1980), pp. 317–322.Google Scholar
3. Donald, J., Elwin, J., Hager, R. and Salamon, P., A graph theoretic bound on the permanent of a nonnegative matrix I & II, Lin. Alg. and Its Applic. 61 (1984), pp. 187–218.Google Scholar
4. Elliot, P. D. T. A., On the number of circles determined by n points, Acta Math. Acad. Sci. Hungar. 18 (1967), pp. 181–189.Google Scholar
5. Erdôs, P., On a problem of Grunbaum, Canad. Math. Bull. 15 (1972), pp. 23–25.Google Scholar
6. Grunbaum, B., Arrangements and spreads, Regional Conference Series in Mathematics, Number 10, Amer. Math. Soc. 1972.Google Scholar
7. Kelly, L. M. and Moser, W., On the number of ordinary lines determined by n points, Canad. J. Math. 10(1958), pp. 210–219.Google Scholar
8. Szemerédi, E. and Trotter, W. T. Jr., Extremal problems in discrete geometry, Combinatorica 3 (1983), pp. 381–392.Google Scholar