Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-14T03:22:20.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Smooth Partitions of Unity on Banach Spaces

Published online by Cambridge University Press:  20 November 2018

R. Fry
R. Fry*
Affiliation:
Department of Mathematics University of Northern British Columbia Prince George, BC V2N 4Z9
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is shown that if a Banach space 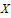$X$ admits a 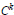${{C}^{k}}$-smooth bump function, and 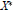${{X}^{*}}$ is Asplund, then 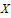$X$ admits 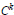${{C}^{k}}$-smooth partitions of unity.

Keywords

46B20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 2 , 01 June 1998 , pp. 145 - 150
Copyright
Copyright © Canadian Mathematical Society 1998

References

[BF] Bonic, R. and Frampton, J., Smooth functions on Banach manifolds. J. Math. Mech. 15 (1966), 877–898.Google Scholar
[DGZ1] Deville, R., Godefroy, G. and Zizler, V., Smoothness and Renormings in Banach spaces. Pitman Monographs Surveys Pure Appl. Math. 64 (1993).Google Scholar
[DGZ2] Deville, R., The three-space problem for smooth partitions of unity and C (K) spaces. Math. Ann. 288 (1990), 613–625.Google Scholar
[EW] Edgar, G. A. and Wheeler, R. F., Topological properties of Banach spaces. Pacific J. Math. 115 (1984), 317–350.Google Scholar
[F] Frontisi, J., Smooth Partitions of Unity in Banach Spaces.Rocky Mountain J.Math. 25 (1995), 1295–1304.Google Scholar
[FG] Fabian, M. and Godefroy, G., The dual of every Asplund space admits a projectional resolution of the identity. Studia Math. 91 (1988), 141–151.Google Scholar
[GTWZ] Godefroy, G., Troyanski, S., Whitfield, J. H. M. and Zizler, V., Smoothness in weakly compactly generated spaces. J. Funct. Anal. 52 (1983), 344–352.Google Scholar
[H] Holmes, R. B., Geometric Functional Analysis and its Applications. Graduate Texts inMath. 24. Springer-Verlag, 1975.Google Scholar
[M1] McLaughlin, D., Smooth partitions of unity on preduals of WCG spaces. Math. Z. 211 (1992), 189–194.Google Scholar
[M2] McLaughlin, D., Smooth partitions of unity and approximating norms in Banach spaces. Rocky Mountain J. Math. 25 (1995), 1137–1148.Google Scholar
[MPVZ] McLaughlin, D., Poliquin, R., Vanderwerff, J., and Zizler, V., Second-Order Gâteaux differentiable bump functions and approximations in Banach spaces. Canad. J. Math. 45 (1993), 612–625.Google Scholar
[P] Phelps, R. R., Convex functions, Monotone operators and differentiablility. Lecture Notes inMath. 1364. Springer-Verlag, 1989.Google Scholar
[R] Rosenthal, H. P., A characterization of Banach spaces containing l1. Proc. Nat. Acad. Sci. U.S.A. 71 (1974), 2411–2413.Google Scholar
[T] Torunczyk, H., Smooth partitions of unity on some nonseparable Banach spaces. Studia Math. 46 (1973), 43–51.Google Scholar
[V] Vanderwerff, J., Smooth approximations in Banach spaces. Proc. Amer.Math. Soc. 115 (1992), 113–120.Google Scholar