Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T19:06:14.785Z Has data issue: false hasContentIssue false
  • English
  • Français

The Smallest Pisot Element in the Field of Formal Power Series Over a Finite Field

Published online by Cambridge University Press:  20 November 2018

A. Chandoul ,
M. Jellali  and
M. Mkaouar
A. Chandoul
Affiliation:
Faculté des Sciences de Sfax, BP 1171, Sfax 3000, Tunisia e-mail: [email protected]@[email protected]
M. Jellali
Affiliation:
Faculté des Sciences de Sfax, BP 1171, Sfax 3000, Tunisia e-mail: [email protected]@[email protected]
M. Mkaouar
Affiliation:
Faculté des Sciences de Sfax, BP 1171, Sfax 3000, Tunisia e-mail: [email protected]@[email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Dufresnoy and Pisot characterized the smallest Pisot number of degree 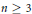$n\,\ge \,3$ by giving explicitly its minimal polynomial. In this paper, we translate Dufresnoy and Pisot’s result to the Laurent series case. The aim of this paper is to prove that the minimal polynomial of the smallest Pisot element 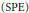$\left( \text{SPE} \right)$ of degree $n$ in the field of formal power series over a finite field is given by 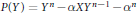$P\left( Y \right)\,=\,{{Y}^{n}}\,-\,\alpha X{{Y}^{n-1}}\,-{{\alpha }^{n}}$ where $\alpha $ is the least element of the finite field 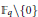${{\mathbb{F}}_{q}}\backslash \left\{ 0 \right\}$ (as a finite total ordered set). We prove that the sequence of SPEs of degree $n$ is decreasing and converges to 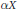$\alpha X$. Finally, we show how to obtain explicit continued fraction expansion of the smallest Pisot element over a finite field.

Keywords

11A5511D4511D7211J6111J66Pisot elementcontinued fractionLaurent seriesfinite fields
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 2 , 01 June 2013 , pp. 258 - 264
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Bateman, P. T. and Duquette, A. L., The analogue of Pisot-Vijayaraghavan numbers in fields of power series. Illinois J. Math. 6(1962) 594–606. Google Scholar
[2] Bertin, M.-J., Decomps-Guilloux, A., Grandet-Hugot, M., Pathiaux-Delefosse, M., and Schreiber, J.-P., Pisot and Salem numbers. Birkhauser Verlag, Basel, 1992.Google Scholar
[3] Chandoul, A., Jellali, M., and Mkaouar, M., Irreducible polynomials and number of Pisot elements. Communications in Algebra, to appear.Google Scholar
[4] Dufresnoy, J. and Pisot, C., Etude de certaines fonctions méromorphes bornées sur le cercle unité. Application á un ensemble fermé d’entiers algébriques. Ann. Sci. Ecole Norm. Sup. (3) 72(1955), 69–92. Google Scholar
[5] Grandet-Hugot, M., Sur une propriété des “nombres de Pisot” dans un corps de série formelles. C. R. Acad. Sér. A-B 266,(1967), A39–A41; errata, ibid. 265(1967), A551.Google Scholar
[6] Grandet-Hugot, M., Nombres de Pisot dans un corps de séries formelles. Séminaire Delange-Pisot-Poitou, Théorie des nombres 8(1966–1967., Exp. No. 4, 1–12. Google Scholar
[7] Grandet-Hugot, M., Eléments algébriques remarquables dans un corps de série formelles, Acta Arith. 14(1967/1968), 177–184. Google Scholar
[8] Hbaid, M. and Mkaouar, M., Sur le bêta développemnt de 1 dans le corps des séries formelles. Int. J. Number Theory 2(2006), no. 3, 365–378. http://dx.doi.org/10.1142/S1793042106000619 Google Scholar
[9] L. Siegel, C., Algebraic number whose conjugates lie in the unit circle. Duke Math. J 11(1944), 597–602. http://dx.doi.org/10.1215/S0012-7094-44-01152-X Google Scholar
[10] Scheicher, K., β-expansion in algebraic function fields over finite fields. Finite Fields Appl. 13(2007), no. 2, 394–410. http://dx.doi.org/10.1016/j.ffa.2005.08.008 Google Scholar
[11] Sprindzuk, V. G., Mahler's problem in metric number theory. Translations of Mathematical Monographs, 25, American Mathematical Society, Providence, RI, 1969.Google Scholar